この記事で解決できる悩み
新NISAで投資を始める前に、オールカントリー(オルカン)やS&P500などの平均利回りに基づいて長期つみたて投資シミュレーションを行うためのツールを作ったので、解説&紹介します。
今回紹介するツールを活用することで、アセットアロケーション分析ができますよ!

[Note] When you can use the tool of English version, please access the following link.
記事前半ではインデックス投資と利回りの関係を、後半ではツール化に向けた対応方針とツールの使い方を解説するので、じっくり読み込んでくださいね!

この記事を書いた人
- 『NISAの達人』の管理人
- 会社員&ブロガー
- 新NISA(選び方、買い方、運用方法、ノウハウ)について発信
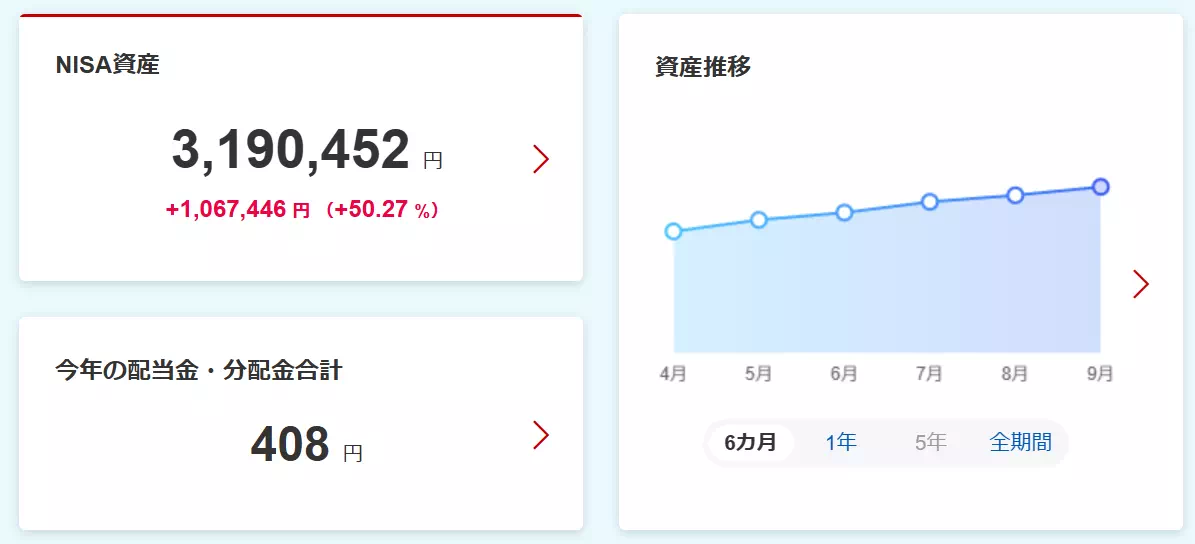
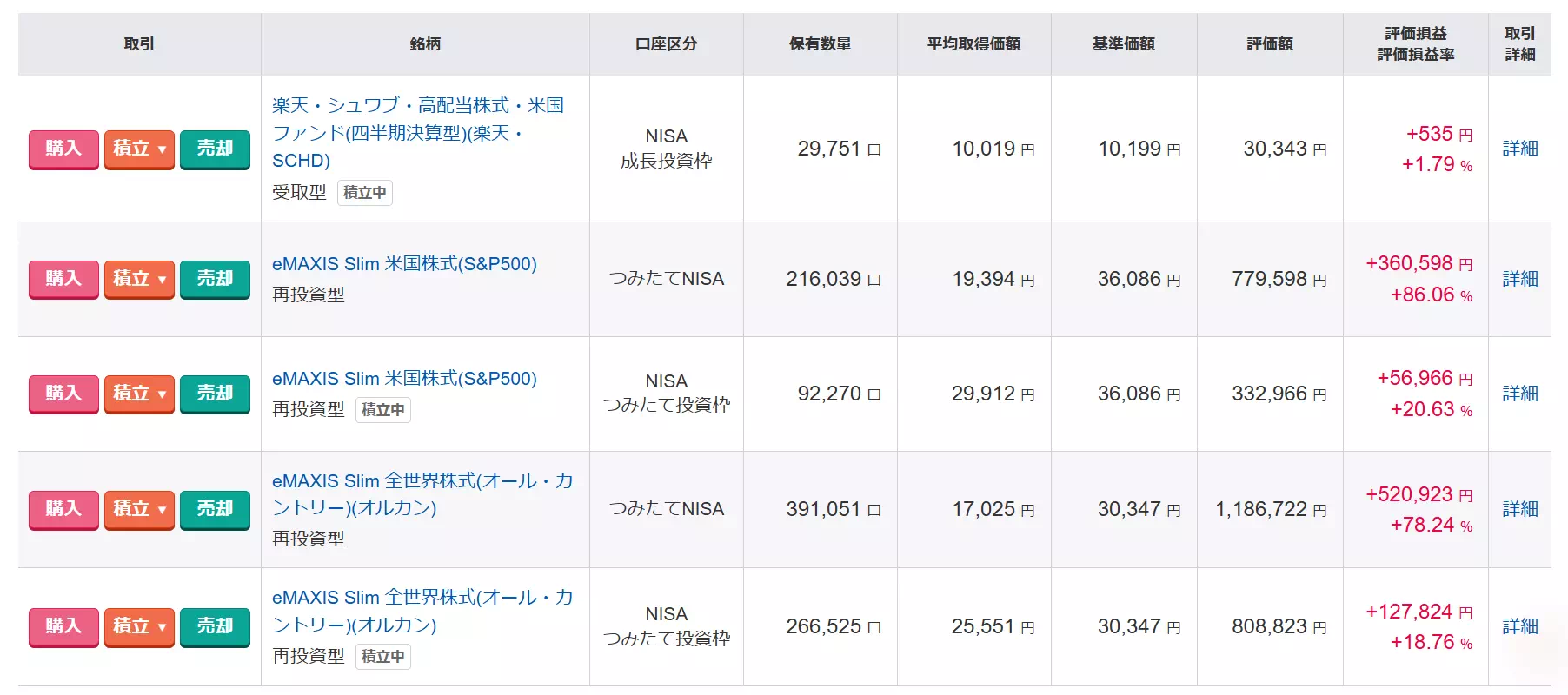
- 2025年9月末時点で、NISAで含み益約106万円を達成中!
この記事を読み終えることで、「インデックス投資と利回りの関係」が理解できるだけではなく、「ツールを活用した長期投資シミュレーション」により将来的な運用成果も見積もることができます。
これから資産運用を始める方
新NISAなど資産運用を始めるには、証券口座の開設が必要です。まだ、証券口座をお持ちでない方は、以下のリンクから口座開設することをおススメします。
-
特徴:取引コストを抑えられる!
-
投資情報や分析ツールが豊富&無料で利用できる!
インデックス投資と利回りについて
まず、以下の4ステップでインデックス投資とインデックス投資の利回りについて解説したいと思います。
インデックス投資とその利回りに関する解説3ステップ
インデックス投資とは?
インデックス投資とは、決められた指数(インデックス)に連動する値動きを目指して投資をする手法のことです。
日本の株式市場と米国の株式市場のそれぞれにおいて、代表的なインデックスは以下のようになります。
| 対象の国 | インデックス |
|---|---|
| 日本 | TOPIX(東証株価指数)や日経平均株価など |
| 米国 | NASDAQ100やS&P500など |
また、上記の株価指数のほかに債券指数やREIT指数などもあり、インデックス投資により様々な資産や幅広い地域への投資ができます。
REIT指数は不動産に関するインデックスです。

インデックス投資では、投資先の銘柄やセクター(業種)が決まっているため、運用時の手数料(信託報酬など)が安く、長期投資に向いている手法と言えます。
インデックス投資の利回りの計算方法
インデックス投資の利回りは、以下の式で計算できます。
$$
\text{利回り} = \dfrac{\text{分配金} + \text{譲渡損益}}{\text{投資額} \times \text{運用年数}} \times 100
$$
分子は投資で得られた利益の合計を表します。

例えば、以下のケースにおける利回りを計算してみましょう。
| 項目 | 値 |
|---|---|
| 分配金 | 1年あたり100円 |
| 譲渡損益 | 10,000円 |
| 投資額 | 30,000円 |
| 運用年数 | 2年 |
この時、下記の計算式から利回りは17%になります。
$$
\begin{eqnarray}
\text{利回り} & = & \dfrac{100 \times 2 + 10,000}{30,000 \times 2} \times 100 \\
& = & \dfrac{5,100}{30,000} \times 100 \\
& = & 17
\end{eqnarray}
$$
記事の後半で、将来の運用結果を見積もる方法をツールと共に紹介しますよ!

インデックス投資の利回りってどの位?
インデックス投資の利回り(リターン)は、投資先の金融商品によって変わります。
利回りは、投資金額に対する収益の割合を表すんでしたね!

なぜなら、評価時点では投資対象の将来的な利益率は分からないためです。
一方、過去実績に基づく利回りであれば、計算することができます。
例えば、1980年1月から2023年12月までにおけるS&P500の利回りは、それぞれ以下のようになります。
| 運用期間 | 利回りの最小値 | 利回りの最大値 |
|---|---|---|
| 1年間 | -38.49% | 34.11% |
| 3年間 | -15.52% | 28.46% |
| 5年間 | -2.24% | 26.32% |
| 10年間 | -1.00% | 16.90% |
| 15年間 | 4.07% | 16.26% |
| 20年間 | 5.13% | 14.67% |
利回りが決まった値ではなく範囲で求まる理由として、1980年1月から2023年12月までのうち、どの部分を運用期間として指定するかにより、結果が異なるためです。
例えば、投資期間を20年間とした場合、利回りの最小値と最大値の期間はそれぞれ以下のようになります。
| 対象 | 開始時期 | 終了時期 |
|---|---|---|
| 利回りの最小値 | 1999年1月 | 2018年12月 |
| 利回りの最大値 | 1980年1月 | 1999年12月 |
また、上記を図で表すと以下のようになります。
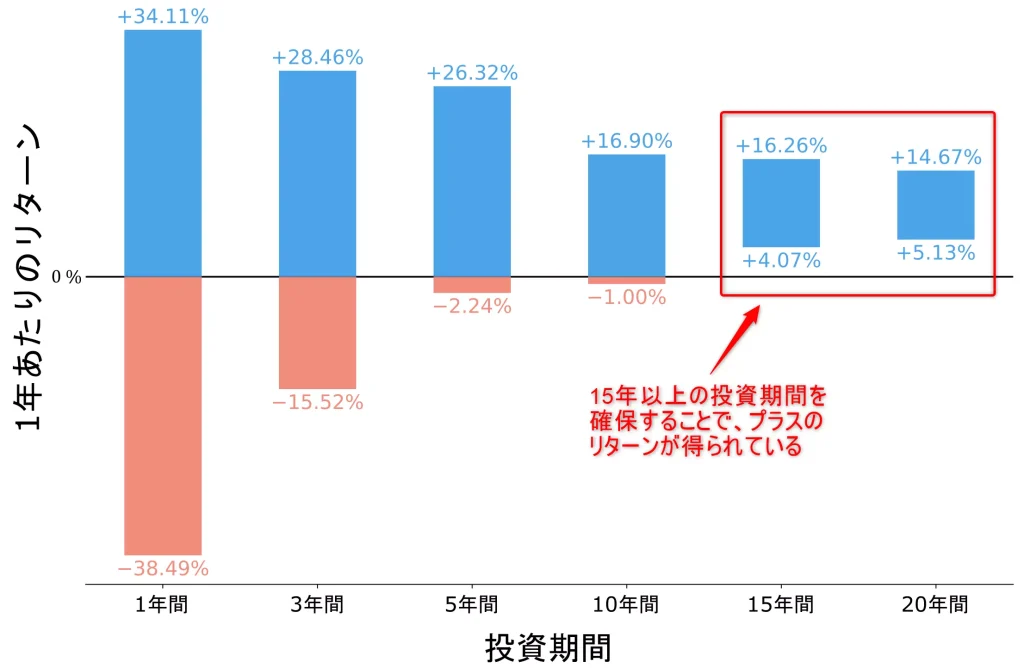
この結果から、投資期間を15年以上確保できれば元本割れする可能性が低そうであることが分かりますね。
投資対象ごとの平均利回り
続いて、以下の2つの観点に基づいて投資対象ごとの平均利回りを紹介したいと思います。
投資対象ごとの平均利回り2パターン
資産ごとの平均利回り
この記事の最初に述べたように、投資時のインデックスとして株価指数、債券指数、REIT指数などがあります。
ここでは、これらの資産ごとの平均利回りを確認しましょう!
三井住友DSアセットマネジメントが公開している「主要アセットクラスの長期パフォーマンス分析」に基づくと、資産ごとの平均利回りは以下のようになっています。
| 対象資産 | 平均利回り |
|---|---|
| 先進国株式 | 8.4% |
| 新興国株式 | 8.1% |
| 世界REIT | 7.2% |
| 世界国債 | 3.7% |
| コモディティ | -4.3% |
コモディティ投資では、金・原油・大豆などの資源が投資対象となりますよ。

この結果から、今後の成長が期待できる投資先は株式であることが分かりますね。
投資信託ごとの平均利回り
インデックス投資を行う場合、投資信託を購入することが多いと思います。
ここでは、投資信託ごとの平均利回りについて紹介します。
用語説明:投資信託とは?
投資信託(ファンド)とは、投資家から集めたお金をひとつの大きな資金としてまとめ、運用のプロであるファンドマネージャーが株式や債券などに投資・運用しその運用の成果として生まれた利益を皆さんに還元するという金融商品です。
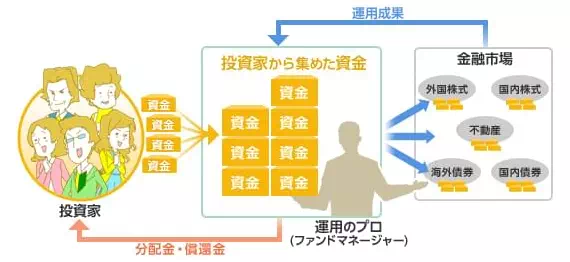
投資信託の仕組み(出典:楽天証券)
今回も楽天証券の投資信託に関するページを参考に、2024年8月16日時点の利回りをまとめました。
投資信託ごとの平均利回りは以下に示す通りです。
| 投資信託 | 対象 | 平均利回り(過去5年間) |
|---|---|---|
| eMAXIS Slim 米国株式(S&P500) | 米国株式 | 23.14 % |
| eMAXIS Slim 全世界株式(オール・カントリー) | 先進国株式・新興国株式 | 19.49% |
| eMAXIS Slim 国内株式(TOPIX) | 日本株式 | 14.85% |
| eMAXIS Slim 先進国債券インデックス | 先進国債券 | 5.09% |
| eMAXIS Slim 国内債券インデックス | 日本債券(日本国内の公社債) | -1.95% |
| eMAXIS Slim バランス(8資産均等型) | 株式、債券、REIT | 8.88% |
以上の結果から、投資信託ごとでも利回りに違いがあることが分かります。
直近5年間はS&P500の投資成績が良いですね!

長期投資シミュレーション
過去実績に基づく利回りを紹介してきましたが、今後の運用成績の見込みも踏まえて投資対象を選びたい方もいると思います。
以降では、先人の知見も活用したツールを用いて長期投資のシミュレーションを行う方法を紹介します。
長期投資シミュレーション:4ステップ
先人の知見紹介
リターン(利回り)とリスクと複利の関係は、先人が知見としてまとめていました。
今回は、こちらの結果を最大限活用したいと思います。
先人の知見2つ
- 連続複利計算
- リターンとリスクの算出
以降では、ツール化する際の最低限の整理を行っています。

連続複利計算
金融工学では、株式や債券、投資信託などの金融商品のリターン(利回り)を分析する際は、リターンが対数正規分布に従うことを仮定します。
金融工学では、正規分布を前提に置いて分析することが一般的であり、オプションの理論価格を求めるブラックショールズモデルも原資産価格のリターンが正規分布する(厳密には、原資産価格自体の変動が対数正規分布する)ことを仮定している。
https://www.nomura.co.jp/terms/japan/se/A02445.html
詳細は省略しますが、上記の仮定は元金 $A$ 円、連続複利のリターンを $r$ としたときに下記が成り立つことを意味しています。
$$
A e^{r}, r \sim \mathcal{N}(\mu, \sigma^{2})
$$
ここで、$A e^{r}$ は連続複利計算の式であり、それぞれの変数の意味は以下の通りです。
| 変数 | 説明 |
|---|---|
| $\mathcal{N}(\cdot)$ | 正規分布 |
| $\mu$ | 正規分布の平均(リターン) |
| $\sigma$ | 正規分布の標準偏差(リスク) |
補足:連続複利計算とは?対数正規分布とは?
- 連続複利計算
連続でなめらかな関数で定義した利息計算
出典:https://www.chart.co.jp/subject/sugaku/suken_tsushin/68/68-2.pdf - 対数正規分布
確率変数の対数をとったとき、対応する分布が正規分布に従うもの

出典:https://en.wikipedia.org/wiki/Log-normal_distribution
以降では、1年あたりのリターンとリスク(年率平均リターンと年率平均リスク)を用いて、積立時点のリターンとリスクの計算方法について説明します。
リターンとリスクの算出
リターンとリスクの計算方法を説明する前に、どの情報に基づいて何を求めたいか、今一度整理しておきます。
私なりの整理結果(イメージ図)は、以下に示す通りです。
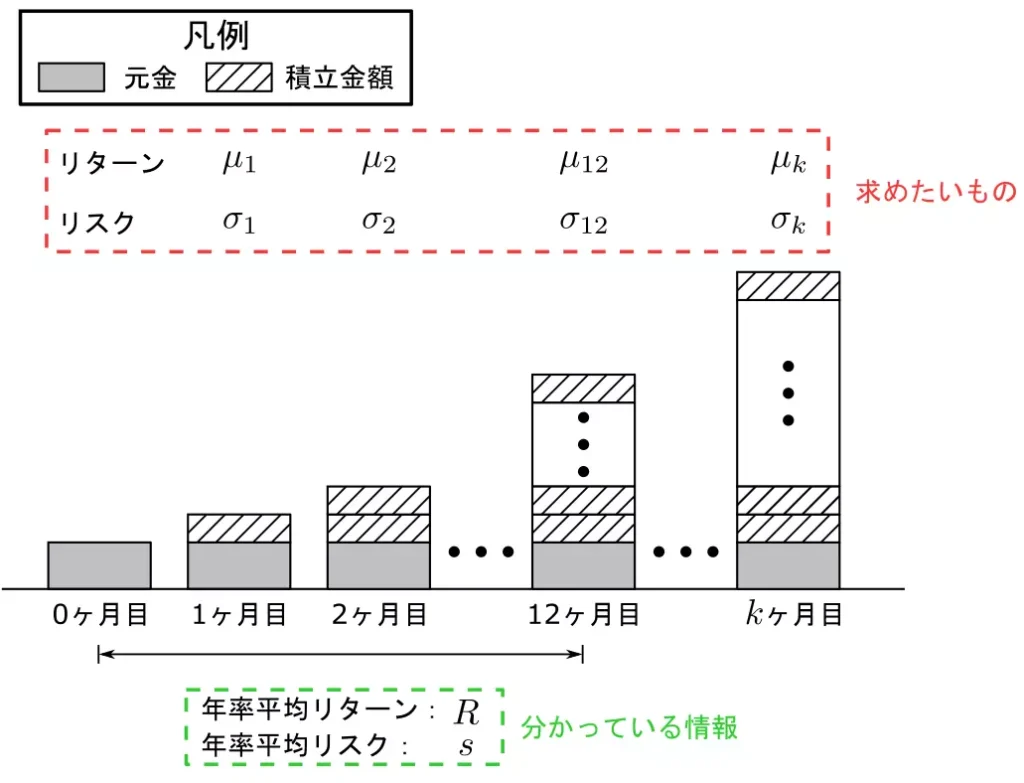
ここで、分かっている情報を一覧化すると以下のようになります。
分かっている情報一覧
- $R$ :年率平均リターン
- $s$ :年率平均リスク
- 運用結果である資産額の分布 $A e^{r}$ は、対数正規分布に従う
- 1年間投資した際の資産額の分布は、平均 $1 + R$、標準偏差 $s$(分散 $s^{2}$)である
上図において、実際は複利による利益も積みあがっていきます。

参照したサイトでは、対数正規分布に従う確率変数 $\log{X} \sim \mathcal{N}(\mu, \sigma^{2})$ の平均 $\mu$ と分散 $\sigma^{2}$ の関係に基づいて、以下が成り立つと整理されています。
$$
\begin{eqnarray}
\mathrm{E}[X] & = & e^{\mu + (\sigma^{2} / 2)} = 1 + R \\
\mathrm{V}[X] & = & e^{2\mu + \sigma^{2}} \left( e^{\sigma^{2}} - 1 \right) = s^{2}
\end{eqnarray}
$$
また、独立な対数正規分布に従う2つの確率変数 $X$ と $Y$ の和も対数正規分布に従うことが知られています。
確率分布の再生性
$\log{X} \sim \mathcal{N}(\mu_{x}, \sigma_{x}^{2}) $、$\log{Y} \sim \mathcal{N}(\mu_{y}, \sigma_{y}^{2})$ とすると、以下が成り立つ。
$$
\log{X} + \log{Y} \sim \mathcal{N}(\mu_{x} + \mu_{y}, \sigma_{x}^{2} + \sigma_{y}^{2})
$$
以上でツール化に必要な準備が整いました。
以降では、上記の関係を用いてツール化に向けた準備を行います。
ツール化に向けた準備
ツール化を行う上で、解消しておく問題が2つ残っています。
解消すべき問題点2つ
- 複数資産を対象としたリターンとリスクの計算方法
株式と債券を50%ずつ運用する場合のリターンとリスクは、どうやって求める? - 積立投資時におけるリターンとリスクの計算方法
$k$ ヶ月目のリターン $\mu_{k}$ とリスク $\sigma_{k}$ は、どうやって求める?
以降では、これらの求め方について解説します。
あわせてjavascriptにおける実装例も紹介しますよ!

複数資産全体のリターンとリスクの計算方法
$n$ 個の資産があり、資産の配分比率、リターン、リスク、相関係数をそれぞれ以下のように定義します。
| 変数 | 定義 |
|---|---|
| $w_{i}$ | $i$ 番目の資産の配分比率 |
| $\alpha_{i}$ | $i$ 番目の資産のリターン |
| $\beta_{i}$ | $i$ 番目の資産のリスク |
| $\gamma_{ij}$ | $i$ 番目の資産と $j$ 番目の資産の相関係数 |
また、資産運用にかかる手数料を $c$ とします。
この時、複数資産全体のリターン $R$ とリスクの2乗 $s^{2}$ は以下のように計算できます。(参考サイト)
$$
\begin{eqnarray}
R & = & \left( \sum_{k = 1}^{n} w_{k}\alpha_{k} \right) - c \\
s^{2} & = & \sum_{k = 1}^{n} (w_{k}\beta_{k})^{2} + 2 \sum_{i = 1}^{n} \sum_{i < j \le n} w_{i}w_{j}\gamma_{ij}
\end{eqnarray}
$$
積立投資時におけるリターンとリスクの計算方法
積立投資において、$k$ ヶ月目のリターン $\mu_{k}$ とリスク $\sigma_{k}$ を計算する必要があります。
また、積み立てにより利息計算の対象が変わるため、これを考慮した更新式も必要です。
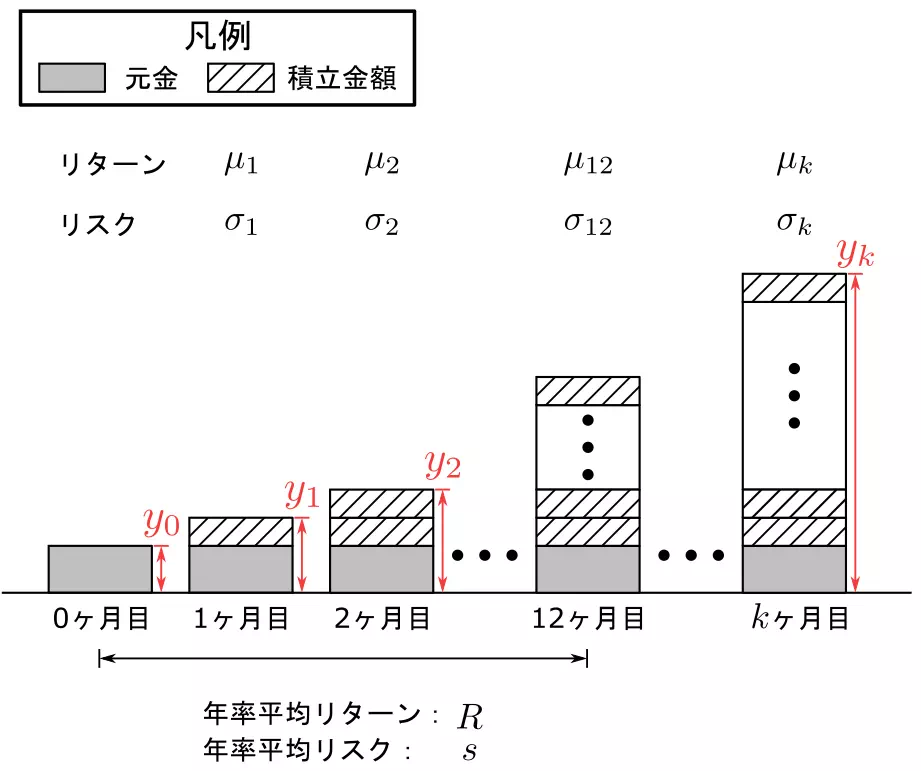
このため、最初に月率リターン $R_{m}$ と月率リスク $s_{m}$ を求めた上で、$\mu_{k}$ と $\sigma_{k}$ に関する更新式を導出します。
まず、毎月の利息計算の関係式から以下が成り立ちます。
$$
\begin{eqnarray}
&& (1 + R_{m})^{12} = 1 + R \\
&& 12 s_{m}^{2} = s^{2}
\end{eqnarray}
$$
$R$ は年率平均リターン、$s$ は年率平均リスクでしたね。

上記を解くことで、月率リターン $R_{m}$ と月率リスク $s_{m}$ を求めることができます。
$$
\begin{eqnarray}
R_{m} & = & -1 + (1 + R)^{1/12} \\
s_{m} & = & \dfrac{s}{\sqrt{12}}
\end{eqnarray}
$$
また、$R$ と $s$、$\mu$ と $\sigma$ の関係から、月率リターン $R_{m}$ と月率リスク $s_{m}$に対する連続複利のリターン $\mu_{m}$ とリスクの2乗 $\sigma_{m}^{2}$ は、それぞれ以下のように計算できますね。
$$
\begin{eqnarray}
\sigma_{m}^{2} & = & \log{\left\{ \dfrac{s_{m}^{2}}{(1 + R_{m})^{2}} + 1 \right\}} \\
\mu_{m} & = & \log{(1 + R_{m})} - \dfrac{\sigma_{m}^{2}}{2}
\end{eqnarray}
$$
次に、毎月の運用成果を表す確率変数を $X_{m}$、$k - 1$ ヶ月目までの運用成果を表す確率変数を $Y_{k - 1}$ とすると、以下が成り立ちます。
$$
\begin{eqnarray}
\log{X_{m}} & \sim & \mathcal{N}(\mu_{m}, \sigma_{m}) \\
\log{Y_{k - 1}} & \sim & \mathcal{N}(\mu_{k - 1}, \sigma_{k - 1})
\end{eqnarray}
$$
また、$k - 1$ ヶ月目までの運用成果とその月の運用成果が独立であると仮定すると、対数正規分布の平均と分散、および対数正規分布の再生性から、 $Z = \log{Y_{k - 1}} + \log{X_{m}}$ の平均と分散は、以下のように計算できます。
$$
\begin{eqnarray}
\mathrm{E}[Z] & = & e^{ (\mu_{k - 1} + \mu_{m}) + \{(\sigma_{k - 1}^{2} + \sigma_{m}^{2}) / 2\} } \\
& = & e^{\mu_{m} + (\sigma_{m}^{2} / 2)} \cdot e^{\mu_{k - 1} + (\sigma_{k - 1}^{2} / 2)} \\
& = & (1 + R_{m}) \mathrm{E}[Y_{k - 1}] \\
\mathrm{V}[Z] & = & e^{ 2(\mu_{k - 1} + \mu_{m}) + \sigma_{k - 1}^{2} + \sigma_{m}^{2} } \left( e^{\sigma_{k - 1}^{2} + \sigma_{m}^{2}} - 1 \right) \\
& = & e^{2\mu_{m} + \sigma_{m}^{2}} \cdot e^{2\mu_{k - 1} + \sigma_{k - 1}^{2}} \left(-1 + e^{\sigma_{k - 1}^{2}} \cdot e^{\sigma_{m}^{2}} \right) \\
& = & (1 + R_{m})^{2} (\mathrm{E}[Y_{k - 1}])^{2} \left[ -1 + \left\{ \dfrac{\mathrm{V}[Y_{k - 1}]}{(\mathrm{E}[Y_{k - 1}])^{2}} + 1 \right\} e^{\sigma_{m}^{2}} \right]
\end{eqnarray}
$$
途中の式変形では、
$$
\begin{eqnarray}
& & \mathrm{V}[Y_{k - 1}] = e^{2\mu_{k -1} + \sigma_{k - 1}^{2}} \left( e^{\sigma_{k - 1}^{2}} - 1 \right) \\
& \Leftrightarrow & \mathrm{V}[Y_{k - 1}] = (\mathrm{E}[Y_{k - 1}])^{2} \left( e^{\sigma_{k - 1}^{2}} - 1 \right) \\
& \Leftrightarrow & e^{\sigma_{k - 1}^{2}} = \dfrac{\mathrm{V}[Y_{k - 1}]}{(\mathrm{E}[Y_{k - 1}])^{2}} + 1
\end{eqnarray}
$$
という関係を使っていますよ!

さらに、$k - 1$ ヶ月目までの運用成果とその月の運用成果の和は、$k$ ヶ月目までの運用成果と等しくなります。
従って、毎月の積立額を $a$ とすると、以下のような更新式を得ることができます。
$$
\begin{eqnarray}
\mathrm{E}[Y_{k}] & \leftarrow & (1 + R_{m}) \mathrm{E}[Y_{k - 1}] + a \\
\mathrm{V}[Y_{k}] & \leftarrow & (1 + R_{m})^{2} (\mathrm{E}[Y_{k - 1}])^{2} \left[ -1 + \left\{ \dfrac{\mathrm{V}[Y_{k - 1}]}{(\mathrm{E}[Y_{k - 1}])^{2}} + 1 \right\} e^{\sigma_{m}^{2}} \right]
\end{eqnarray}
$$
0ヶ月目の場合は元金を $A$ 円として、$\mathrm{E}[Y_{0}] = A$、$\mathrm{V}[Y_{0}] = 0$ と表現できますよ。

実装例
導出した関係式を用いて、年率平均リターン $R$ と年率平均リスク $s$ から毎月のリターンとリスクを推定するプログラムを作成したいと思います。
javascriptによる実装例は、以下に示す通りです。
/**
* @brief 年率平均リターンと年率平均リスクから月率リターンと月率リスクを計算
* @param[in] averageReturn 年率平均リターン
* @param[in] averageRisk 年率平均リスク
*/
const calculateReturnAndRisk = (averageReturn, averageRisk) => {
const monthlyReturn = Math.pow(1 + averageReturn, 1.0 / 12.0) - 1;
const monthlyRisk = averageRisk / Math.sqrt(12.0);
const ret = {
return: monthlyReturn,
risk: monthlyRisk,
};
return ret;
};
/**
* @brief 対数正規分布の平均と標準偏差
* @param[in] targetReturn リターン
* @param[in] targerRisk リスク
*/
const calculateMuAndSigma = (targetReturn, targerRisk) => {
const variance = Math.log(Math.pow(targerRisk / (1 + targetReturn), 2.0) + 1);
const ret = {
mu: Math.log(1 + targetReturn) - 0.5 * variance,
sigma: Math.sqrt(variance),
};
return ret;
};
/**
* @brief 毎月のパフォーマンス(リスクとリターン)の計算
* @param[in] monthlyInvestment 毎月の積立額
* @param[in] monthlyReturn 毎月のリターン
* @param[in] monthlyRisk 毎月のリスク
* @param[in] totalReturn 先月までのリターン
* @param[in] totalRisk 先月までのリスク
*/
const calculatePerformance = (monthlyInvestment, monthlyReturn, monthlyRisk, totalReturn, totalRisk) => {
const estimatedReturn = (1 + monthlyReturn) * totalReturn + monthlyInvestment;
// 0で割る操作を回避するため、微小定数(1e-7)を加算して計算
const estimatedRisk = (1 + monthlyReturn) * totalReturn * Math.sqrt(
-1 + (Math.pow(totalRisk / (totalReturn + 1e-7), 2.0) + 1) * Math.exp(monthlyRisk * monthlyRisk)
);
const current = calculateMuAndSigma(estimatedReturn, estimatedRisk);
const ret = {
totalReturn: estimatedReturn,
totalRisk: estimatedRisk,
return: current.mu,
risk: current.sigma,
};
return ret;
};長期投資シミュレーションツール
今回作成したツールを紹介します。
リターン、リスク、相関係数はそれぞれ、年金積立金管理運用独立行政法人(GPIF)の資料を参考に設定しております。

また、6月と12月の年2回をボーナス月とみなして、シミュレーションを行います。
| 具体的な操作方法 | 見た目の変化 |
|---|---|
| Ctrlキーを押しながらマウススクロール | 拡大・縮小 |
| Ctrlキーを押しながらドラッグ&ドロップ | グラフの移動 |
| ドラッグ&ドロップ | 選択範囲の拡大・縮小 |
| ピッチ操作(スマホ・タブレット) | 拡大・縮小 |
【参考】ツールによるシミュレーションができない場合
稀に、プログラムの読み込みに失敗し、シミュレーションができないことがあるみたいです。
この場合、ページをリロード(再読み込み)してみてください。
シミュレーションツールの使い方
まず、基本設定の項目にて、元金、毎月の積立額、投資期間、手数料を入力してください。

今回は、手数料のみを更新しました。

次に、各種資産の設定にて、各種資産の配分比率、期待リターン、リスクを設定します。
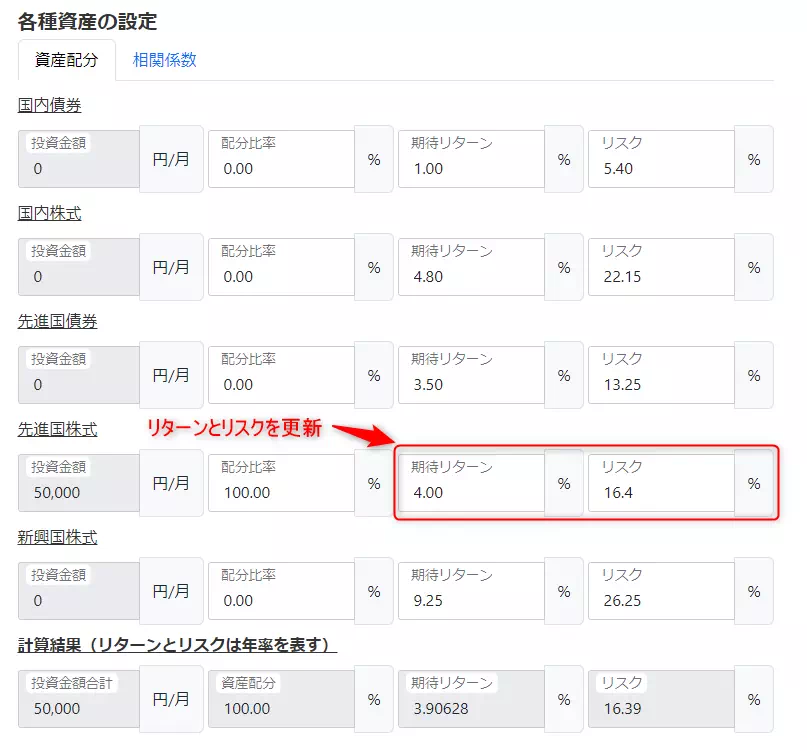
期待リターンやリスクは、過去実績に基づいて設定してください。

上記を設定すると、シミュレーション結果が得られます。
各種資産の割合
各種資産の割合は、円グラフから確認できます。
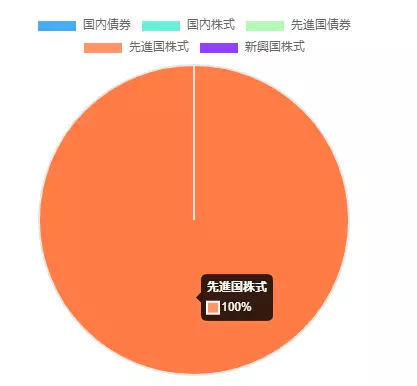
投資結果
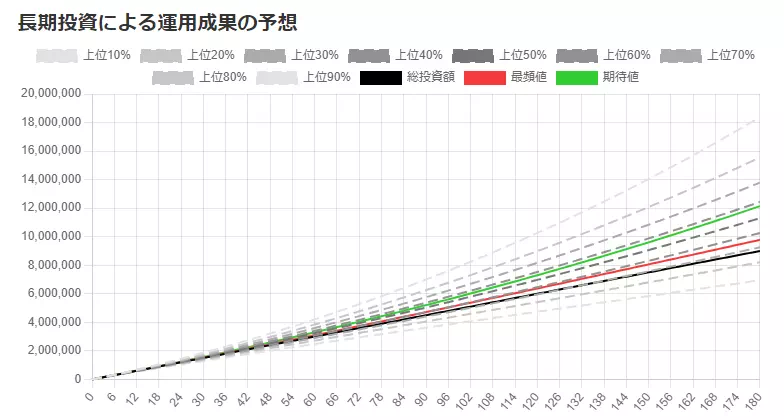
投資結果も以下のような折れ線グラフで表示されるようにしました。

この折れ線グラフは、Ctrlを押しながらマウススクロールすることで、拡大縮小もできます。
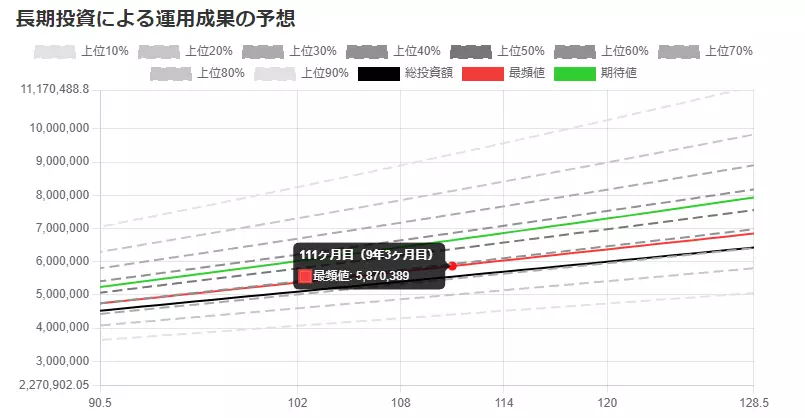
Ctrlキーを押しながらドラッグ&ドロップすることで上下左右移動もできます。

また、代表的な数値(期待値、中央値、最頻値)も確認できるようにしました。
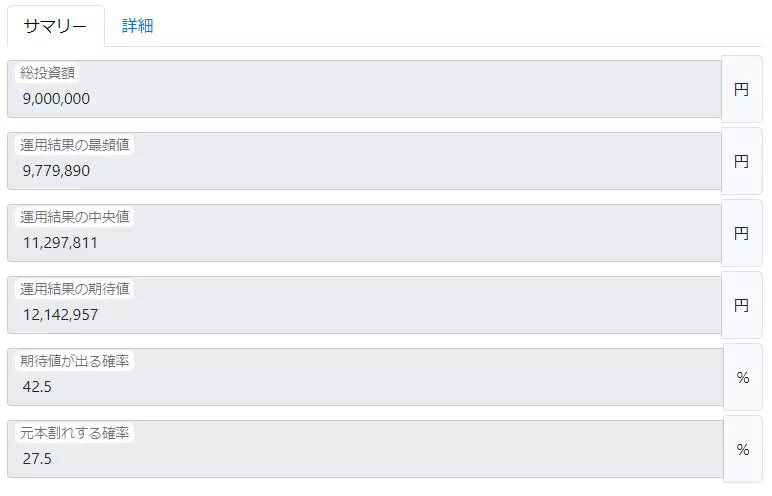
事前に長期投資の成果を確認しよう!
今回は、以下について解説しました。
資産運用は、長期・積立・分散の3本柱で進めていくことが鉄則となりますが、その一方で将来的にどの程度資産が増えるかは未知数です。
このため、今回は利回りの解説から始まり、ツールによるシミュレーションもできるようにしました。
今回ご紹介したツールを活用し、将来的な資産の見積もりをしてみてください。

シミュレーション結果をもとに、ご自身の経済状況やライフプランにあわせて、投資先や運用方法を決めることをおすすめします!
これから資産運用を始める方
新NISAなど資産運用を始めるには、証券口座の開設が必要です。まだ、証券口座をお持ちでない方は、以下のリンクから口座開設することをおススメします。
-
特徴:取引コストを抑えられる!
-
投資情報や分析ツールが豊富&無料で利用できる!

