S&P500の期待リターンと想定リスクは？計算方法と導出例を解説

今回は、期待リターンと想定リスクの計算方法とその活用例について解説します。

記事の前半では投資におけるリターンとリスクの意味、および、期待リターンと想定リスクの導出う方法を解説します。

後半では過去150年以上のデータを用いて導出した期待リターンと想定リスクの結果とそれらの活用方法を具体的に解説します。

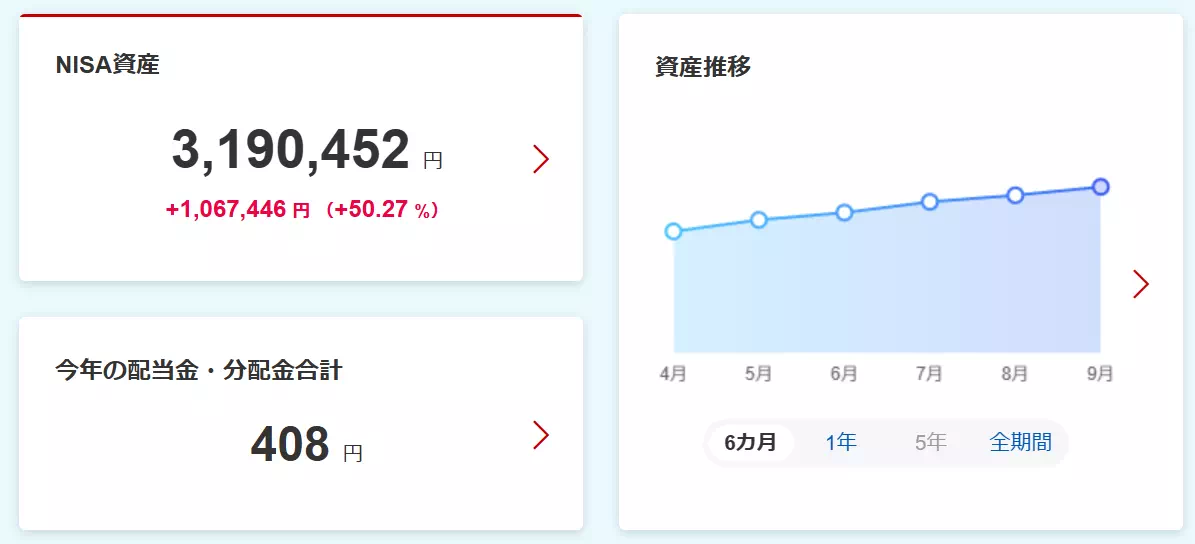
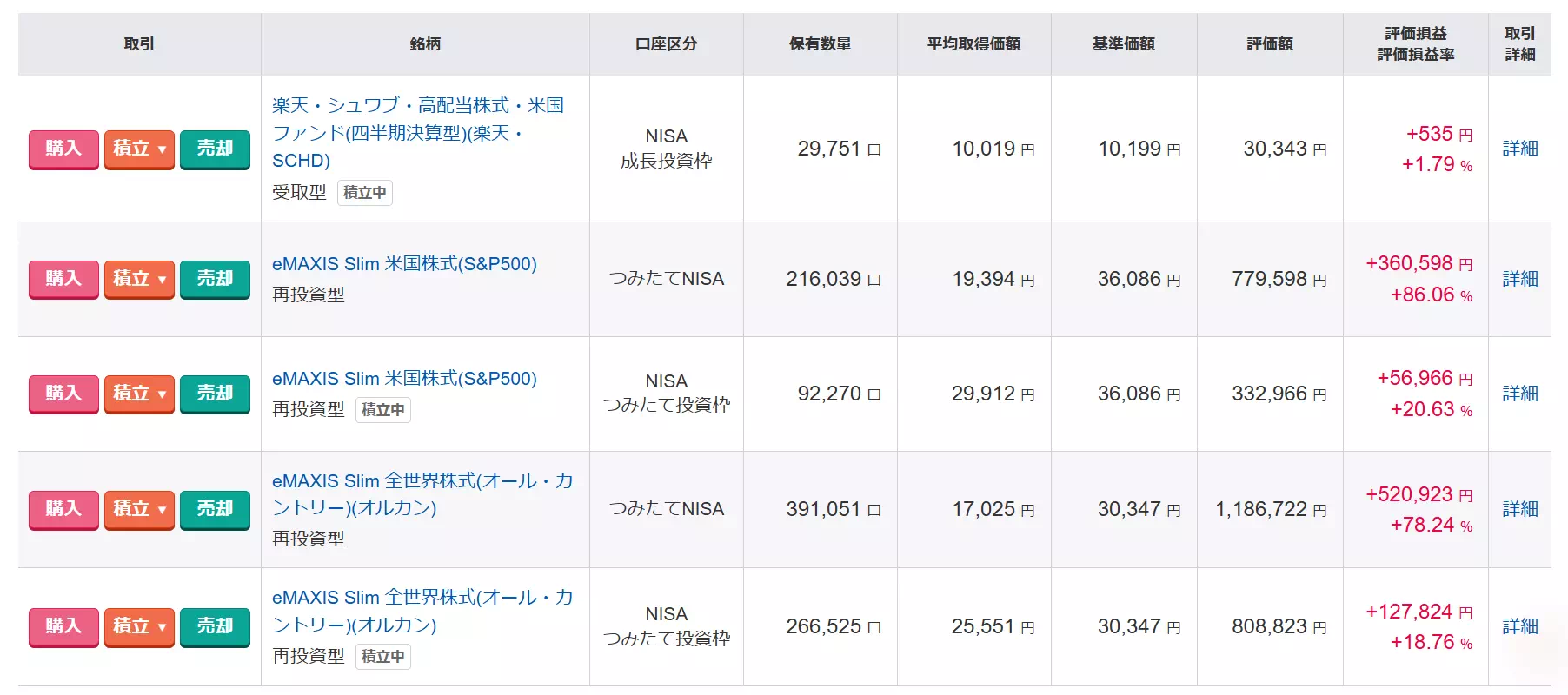
この記事を読み終えることで、「S&P500の期待リターンと想定リスク」の求め方が分かるだけではなく、これらの結果をどのように活用すれば良いかも理解できますよ。

≫松井証券で証券口座を開設する！

投資のリターンとリスクって何？

株式や債券など、特定の金融商品に投資した際の収益率を予測する場合、正規分布というものを仮定することが一般的です。

この正規分布には、リターン（平均値 $\mu$）とリスク（標準偏差 $\sigma$）の2つのパラメータで予測分布全体を表現できるという特徴があります。

まずは、正規分布のパラメータ、リターンとリスクについて簡単に解説します。

リターンとは？

リターンとは、一定期間（1ヶ月間や1年間など）の収益率のことを指します。

リターンのイメージは、以下に示す通りです。

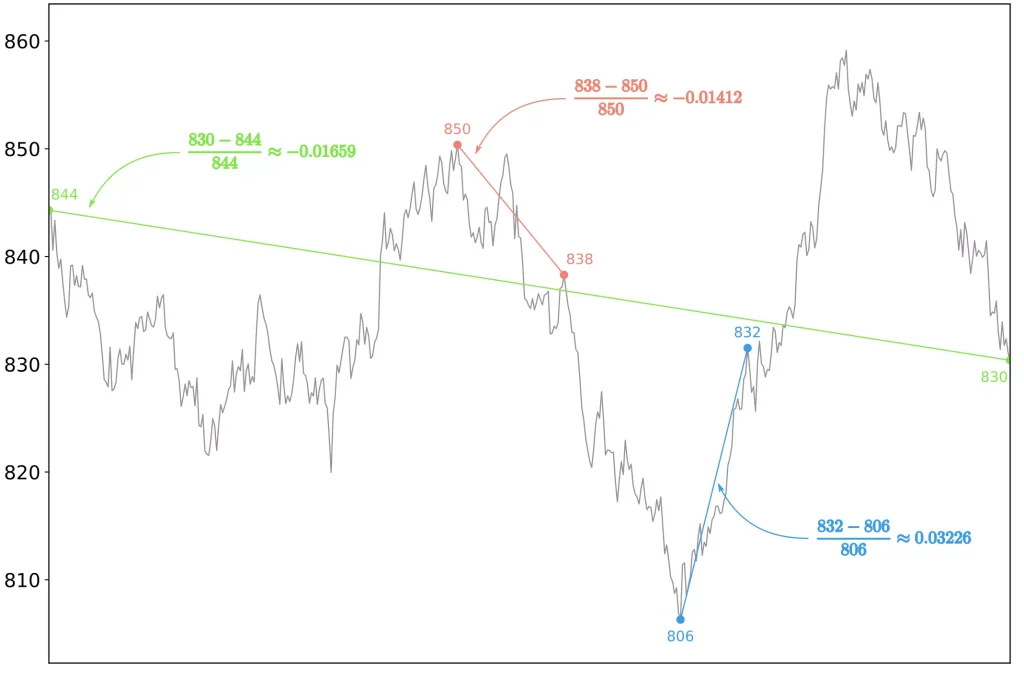
上記の図から、緑色の線や赤色の線は収益が下がっており、青色の線は収益が上がっていることが分かりますね。

このように、集計区間によってリターンの値は変わり得ることを覚えておいて下さい。

また、期待リターンは、将来予想されるリターンの平均値を意味します。

リスクとは？

リスクとは、リターンの振れ幅のことを指します。

リスクのイメージは、以下に示す通りです。

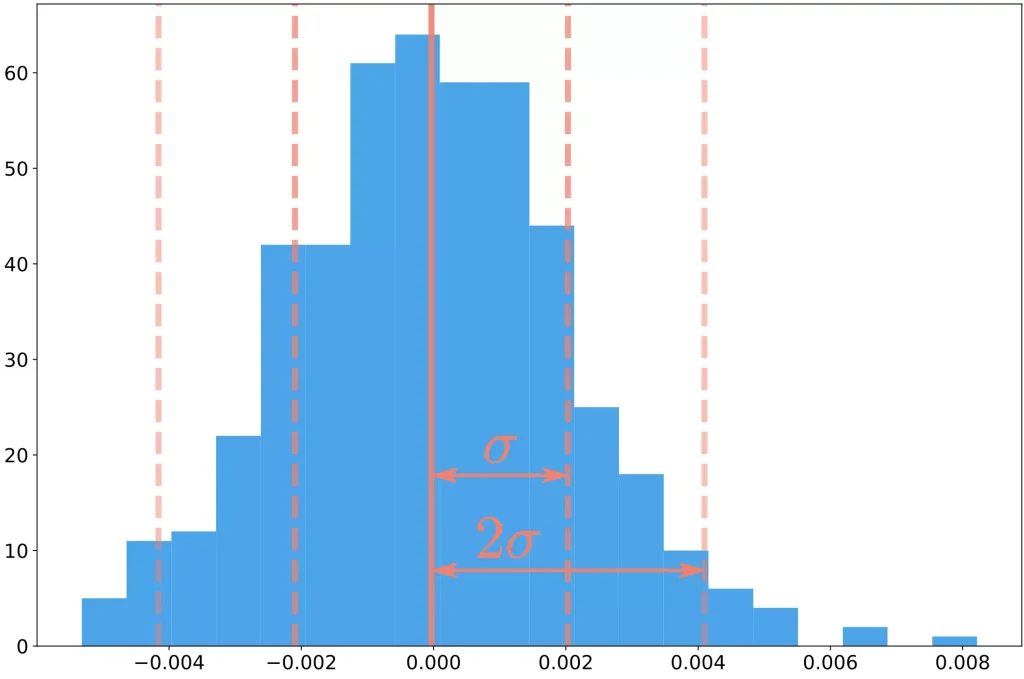
表示されているデータをなるべくカバーしようとすると、振れ幅を大きくとる必要があります。

このように、「ある範囲に収まる確率は、この位である」という見積もりをする上で、リスクは役立ちます。

リターンとリスクの視覚的な理解

株価と正規分布の関係を視覚的に理解するため、イメージ図を用意しました。

①4日分の株価、②過去データに基づいて求めたいパラメータの2つをまとめて記載すると、以下のようになります。

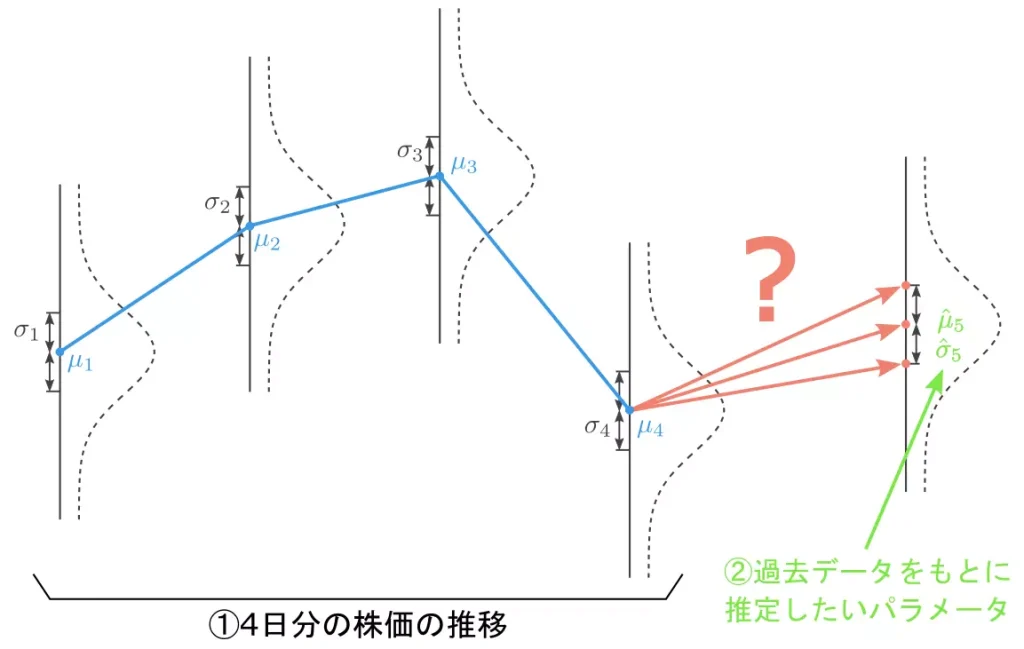
図に示す通り、過去数十年の株価データを用いて、今後のリターンやリスクを推定することが今回やりたいことになります。

さらに、正規分布のパラメータを推定できれば、損失が発生する確率も見積もることができます。

期待リターンと想定リスクの計算方法4ステップ

先程の説明で、リターンとリスクについて概要レベルでは理解できたと思います。

以降では、過去データから期待リターンと想定リスクを計算する方法について解説します。

まず、解説時に登場する変数を把握しておいた方が良いため、一覧を以下にまとめました。

変数	変数の説明	例や備考
$i$	特定の時期を表す変数	3ヶ月目という時の「3」が該当する。$(1 \le i)$
$n$	ある時期から数えて一定期間後を表す変数	5か月後という時の「5」が該当する。$(1 \le n)$
$x_{i}$	$i$ ヶ月目の株価	入力となるデータ
$r_{i}$	$i$ ヶ月目の（月率）リターン	入力データから算出できる値
$R_{n}$	1ヶ月目から数えて $n$ ヶ月後の累積リターン	今回求めるパラメータ
$\widehat{\mu}_{n}$	$n$ ヶ月間の年率平均リターン（期待リターン）	今回求めるパラメータ
$S_{n}$	1ヶ月目から数えて $n$ ヶ月後の累積リスク	今回求めるパラメータ
$\widehat{\sigma}_{n}$	$n$ ヶ月間の年率平均リスク（想定リスク）	今回求めるパラメータ

これらの変数を用いて、下記の4ステップで期待リターンと想定リスクを計算します。

累積リターン

今回は、以下に示す図を参考にしながら、累積リターンを算出した後に年率平均リターン（期待リターン）を計算する方法について解説します。

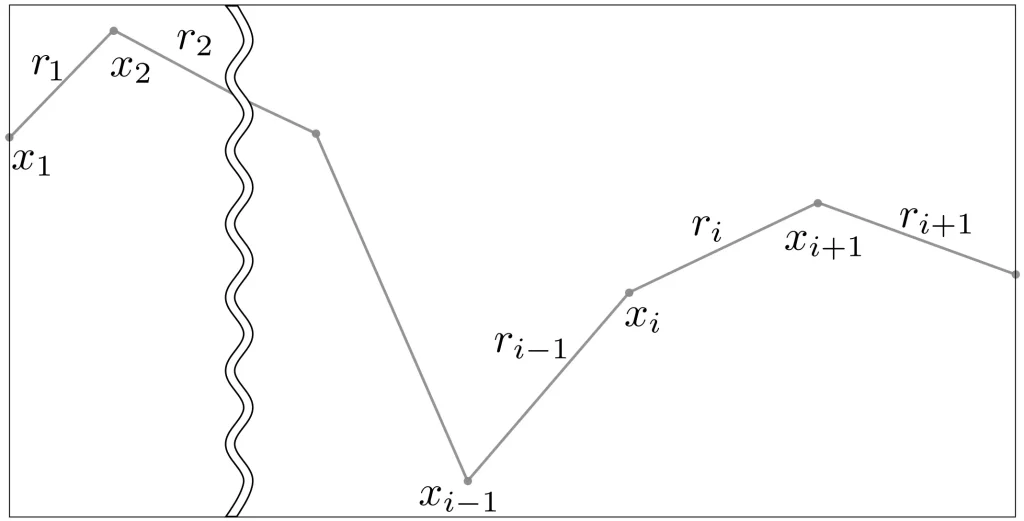
まず、図より、$i$ ヶ月目と $i+1$ ヶ月目の株価の関係は、以下の形式で定式化できます。

$$
x_{i + 1} = (1 + r_{i}) x_{i}
$$

上記を $r_{i}$ について解くと、

$$
r_{i} = \dfrac{x_{i+1} - x_{i}}{x_{i}}
$$

となりますね。

次に、上記の関係から $n$ ヶ月後の株価は、

$$
\begin{eqnarray}
x_{n + 1} & = & (1 + r_{n}) x_{n} \\
& = & (1 + r_{n})(1 + r_{n - 1}) x_{n - 1} \\
& = & (1 + r_{n})(1 + r_{n - 1}) \cdots (1 + r_{1}) x_{1}
\end{eqnarray}
$$

と計算できます。

さらに、累積リターン $R_{n}$ を用いると、上記の株価は $x_{n + 1} = (1 + R_{n}) x_{1}$ とも表現できますね。

以上より、累積リターンは以下のように計算できますよ！

$$
R_{n} = -1 + \prod_{i = 1}^{n} (1 + r_{i})
$$

年率平均リターン（期待リターン）

累積リターンを1ヶ月単位の指標にスケーリングすることで、平均リターンが求まります。

平均リターンのイメージは、以下に示す通りです。

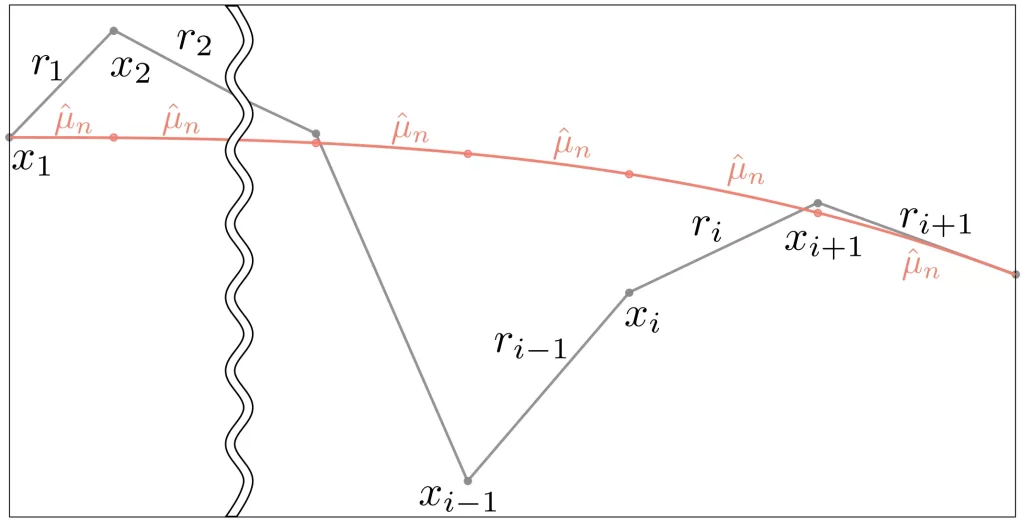
また、リターンは年率で表すことが多いため、平均リターンを12乗することで、年率平均リターン（期待リターン）を求めることができますよ。

上記の操作を数式で表現し、年率平均リターン $\widehat{\mu}_{n}$ を計算した結果は、以下に示す通りです。

$$
\widehat{\mu}_{n} = -1 + \left( 1 + R_{n} \right)^{\frac{12}{n}}
$$

上記の計算を行うことで、累積リターンと年率平均リターン（期待リターン）を算出できることが分かりました。

累積リスク

累積リスクを計算するために、ベースとなる分散を計算します。

下記に示すように、分散を計算する際は、$n$ ヶ月間のそれぞれの月率リターン $r_{i}$ を確率変数として捉え、その総和の散らばりを計算することになります。

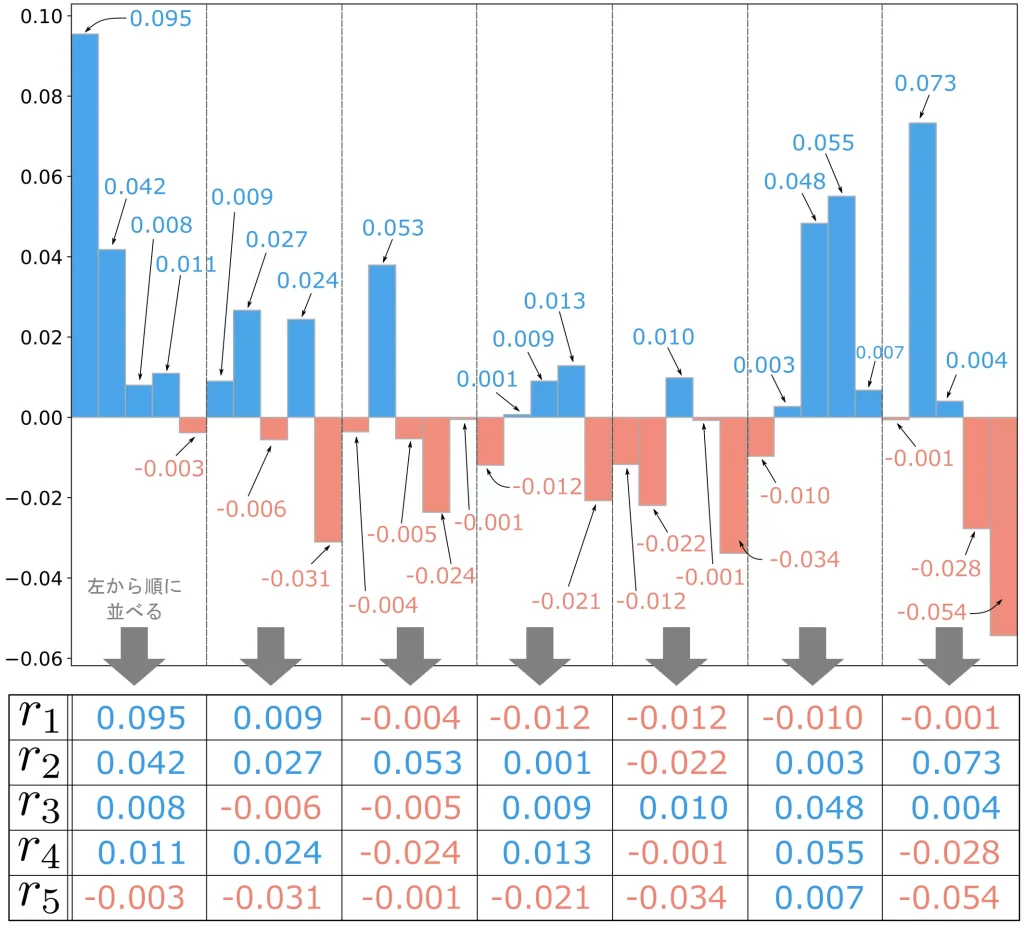
上記を数式で表した結果は、以下に示す通りです。

$$
V\left[ \sum_{i = 1}^{n} r_{i} \right] = \sum_{i = 1}^{n} V[r_{i}] + 2 \sum_{i < j} Cov(r_{i}, r_{j})
$$

ここで、$Cov(r_{i}, r_{j})$ は、$r_{i}$ と $r_{j}$ の共分散を表します。

さらに、この正の平方根が累積リスク $S_{n}$ となるので、求める累積リスクは、以下のように推定できます。

$$
S_{n} = \sqrt{V\left[ \sum_{i = 1}^{n} r_{i} \right]}
$$

年率平均リスク（想定リスク）

上記で求めた分散を1ヶ月単位の指標にスケーリングして正の平方根を取ることで、平均リスクが求まります。

また、リスクも年率で表すことが多いため、これを踏まえて表現した年率平均リスク（想定リスク）は、以下に示す通りです。

$$
\widehat{\sigma}_{n} = \sqrt{\dfrac{12}{n}} S_{n}
$$

ここまでで、期待リターンと想定リスクを求めるための準備が整いました。

試算ツールあり！S&P500の期待リターンと想定リスク

先ほど導出した結果に基づいて、S&P500の過去データの累積リターン、年率平均リターン（期待リターン）、累積リスク、年率平均リスク（想定リスク）を計算してみましょう。

順に解説しますね。

過去150年以上のデータを活用

今回はONLINE DATA ROBERT SHILLERで公開されているデータのうち、1871年1月から2024年11月までの約153年分（1847ヶ月分）のデータを用います。

データの一部をピックアップした結果は、以下に示す通りです。

日付	S&P500インデックス	消費者物価指数	実質トータルリターン
1871/1/1	4.44	12.46	112.54
1871/2/1	4.50	12.84	111.22
1871/3/1	4.61	13.03	112.80
1871/4/1	4.74	12.56	120.93
1871/5/1	4.86	12.27	127.44
1871/6/1	4.82	12.08	128.95
1871/7/1	4.73	12.08	127.13
$\vdots$	$\vdots$	$\vdots$	$\vdots$

また、期待リターンと想定リスクを計算する際の月率リターンに余りが生じる場合、余った分を考慮した移動平均法を用いて推定値を計算しました。

S&P500の累積リターン

今回は、①全期間（1871/1/1～2024/11/1）、②1873/1/1～1947/12/31の75年間、③1924/1/1～2023/12/31の100年間の3パターンに分けて推定を行いました。

推定結果は、以下のようになりました。

区間 [ヶ月]	区間 [年]	①全期間（1871/1/1～2024/11/1）	②1873/1/1～1947/12/31の75年間	③1924/1/1～2023/12/31の100年間
1	0.083	0.825946	0.664142	0.909413
3	0.25	2.583322	2.180972	2.916932
6	0.5	5.247589	4.358782	5.835361
12	1	10.939241	8.812852	11.959074
36	3	35.238438	29.232589	39.262169
60	5	65.843774	52.030305	72.246492
120	10	161.232817	108.685587	201.236918
180	15	327.406142	188.859895	399.324954
240	20	605.940051	292.009775	797.42601
360	30	1621.171558	667.682515	1858.327772
600	50	11276.32752	-	-

推定対象とする区間に注目すると、区間が広いほど累積リターンの値が大きくなることが分かりますね。

S&P500の年率平均リターン（期待リターン）

続いて、年率平均リターン（期待リターン）の推定を行った結果は、以下に示す通りです。

区間 [ヶ月]	区間 [年]	①全期間（1871/1/1～2024/11/1）	②1873/1/1～1947/12/31の75年間	③1924/1/1～2023/12/31の100年間
1	0.083	28.603581	37.079148	36.037687
3	0.25	15.257834	16.512946	18.948791
6	0.5	12.231078	10.834936	13.753533
12	1	10.939241	8.812852	11.959074
36	3	9.695369	7.638662	10.59483
60	5	9.498193	7.319261	10.255496
120	10	9.289125	7.25957	10.377224
180	15	9.261917	6.961806	10.300794
240	20	9.214155	6.948232	10.628948
360	30	9.228617	6.944891	10.227386
600	50	9.220728	-	-

区間の切り取り方に依存しますが、30年間投資を続けると概ね7%～10%のリターンが期待できることが分かりますね。

S&P500の累積リスク

続いて、累積リスクの推定結果を以下に示します。

区間 [ヶ月]	区間 [年]	①全期間（1871/1/1～2024/11/1）	②1873/1/1～1947/12/31の75年間	③1924/1/1～2023/12/31の100年間
1	0.083	4.048628	4.600908	4.459257
3	0.25	8.16261	9.913022	9.600846
6	0.5	11.809599	13.808463	13.100694
12	1	17.788833	18.836671	18.174432
36	3	26.846047	33.819056	29.720567
60	5	35.631496	40.727243	37.334858
120	10	39.599437	30.548694	49.286208
180	15	51.133096	42.419468	52.770248
240	20	62.358867	34.877269	60.784361
360	30	73.588427	32.877682	24.739708
600	50	126.41614	-	-

推定対象とする区間に注目すると、区間を広いほど累積リスクの値が大きくなることが分かりますね。

S&P500の年率平均リスク（想定リスク）

最後に、年率平均リスク（想定リスク）の推定を行った結果を以下に示します。

区間 [ヶ月]	区間 [年]	①全期間（1871/1/1～2024/11/1）	②1873/1/1～1947/12/31の75年間	③1924/1/1～2023/12/31の100年間
1	0.083	14.02486	15.938014	15.447318
3	0.25	16.325219	19.826044	19.201692
6	0.5	16.701295	19.528116	18.527179
12	1	17.788833	18.836671	18.174432
36	3	15.499572	19.525441	17.159177
60	5	15.934889	18.213777	16.696656
120	10	12.522441	9.660345	15.585668
180	15	13.202509	10.95266	13.625219
240	20	13.943867	7.798795	13.591796
360	30	13.435347	6.002616	4.516832
600	50	17.877942	-	-

集計する区間にも依りますが、外れ値っぽいものを除くと10%～20%のリスクがあることが分かりますね。

試算ツール

実際に集計期間や区間を変更して、期待リターンと想定リスクを計算したい方もいると思います。

それを踏まえて、試算するためのツールを作成いたしました。

---

試算ツールの使い方

先ほど紹介した試算ツールの使い方を以下の2ステップで解説します。

条件の設定方法

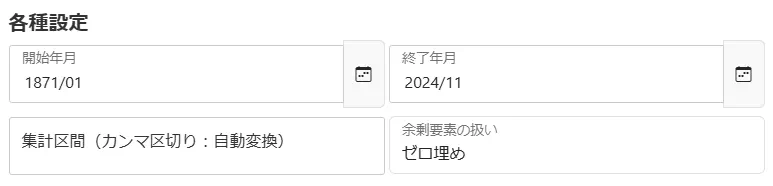
まず、集計に必要な情報の入力方法について解説します。

開始年月と終了年月

参照したい過去データの範囲を指定するため、下記を参考に「開始年月」と「終了年月」に使いたいデータの年月を入力してください。

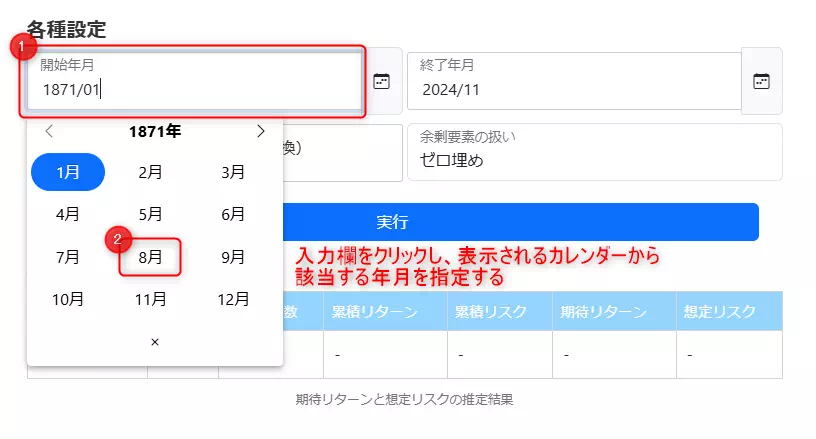
上記の場合、1871年8月から2024年11月の過去データを用いて推定を行うことになります。

集計区間

次に、集計区間をカンマ区切りで入力します。

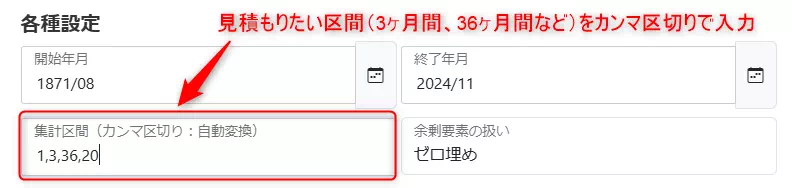
本記事と同じ期間を指定したい場合、1,3,6,12,36,60,120,180,240,360,600 を指定することになります。

余剰要素の扱い

最後に余剰要素の扱い方を指定します。

それぞれの違いは、以下に示す通りです。

余剰要素の扱い方	説明
集計対象外	余剰要素を無視した上で、集計を行います。
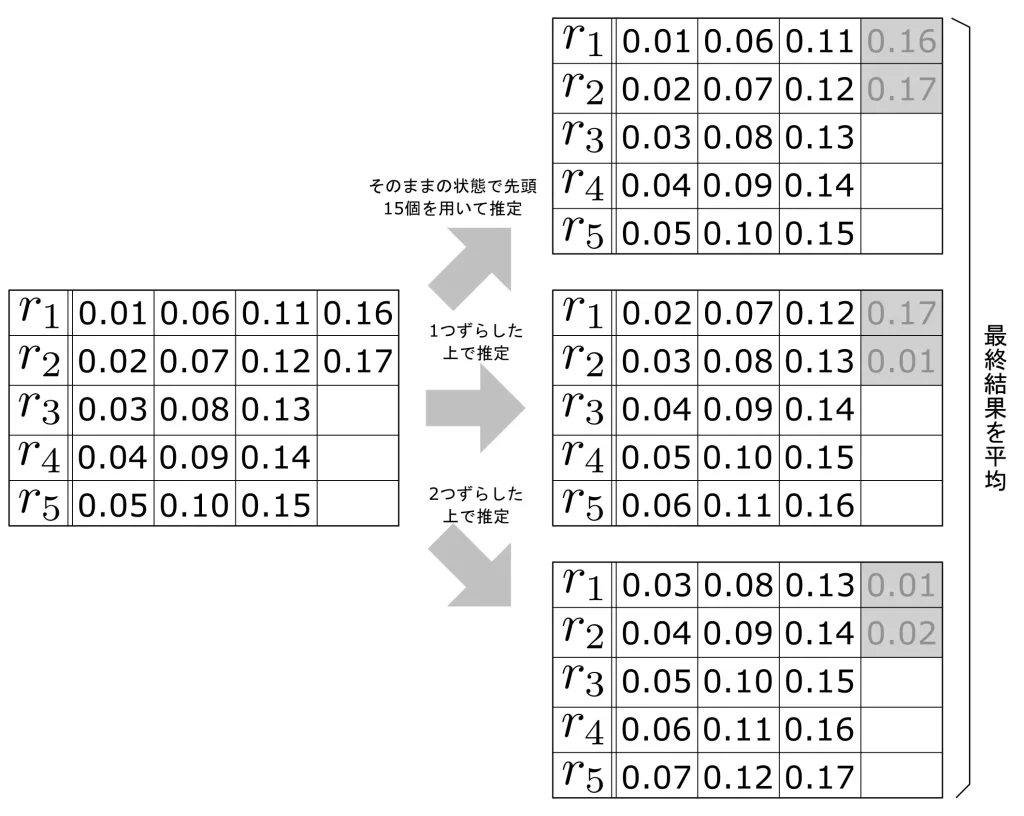
移動平均処理	余剰要素分だけ開始位置をずらしながら集計し、最後に平均を取ります。
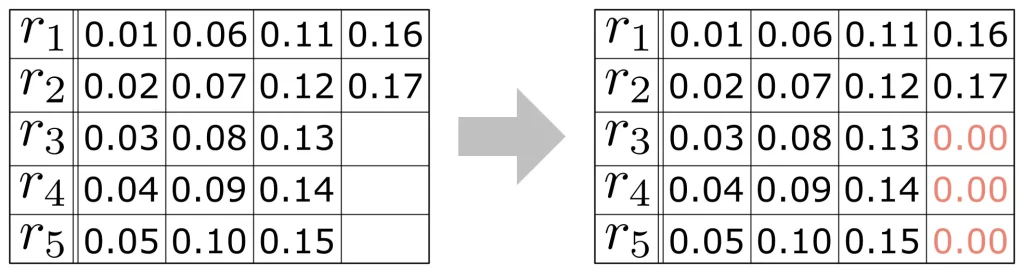
ゼロ埋め	不足部分をゼロで埋めた上で、集計を行います。

視覚的に理解していただくため、それぞれの処理イメージを図で表現してみました。参考にしてください。

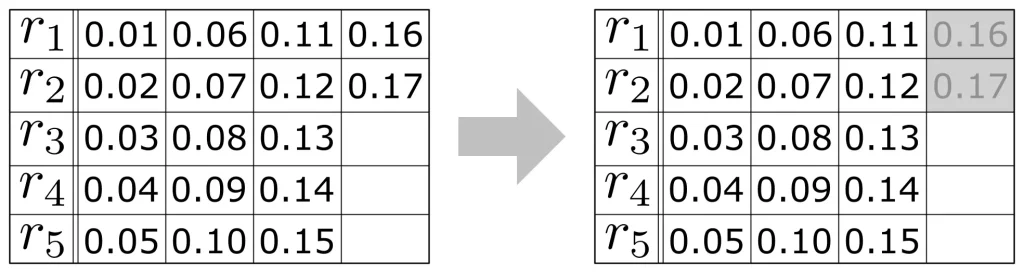
一通り設定が終わったら、「実行」をクリックして下さい。

結果の確認方法

「実行」をクリックした後、しばらくすると以下のような結果が出力されます。

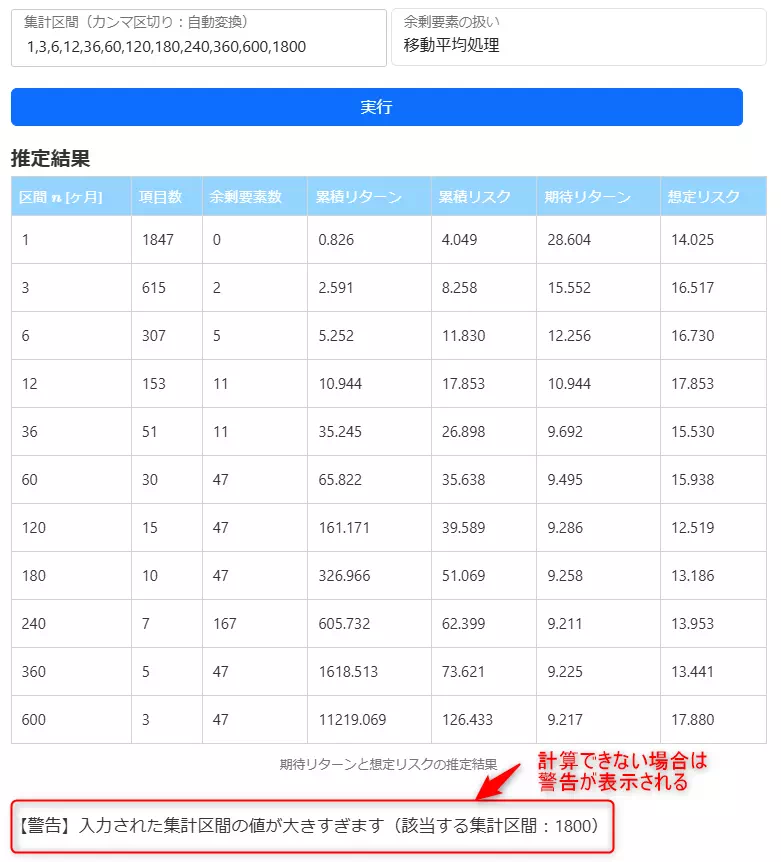
画像中にも記載がありますが、入力された集計区間 $n$ に対して、データ数が足りない場合、その旨を警告するようにしました。

期待リターンと想定リスクの活用方法2つ

最後に、今回求めた期待リターンと想定リスクの活用方法を2つご紹介します。

残りの投資期間が長い場合

残りの投資期間が15年以上ある場合、株式投資を中心としたインデックス投資により資産運用することをおすすめします。

何故なら、15年以上の投資期間が確保できれば、元本割れする確率が極めて小さいからです。

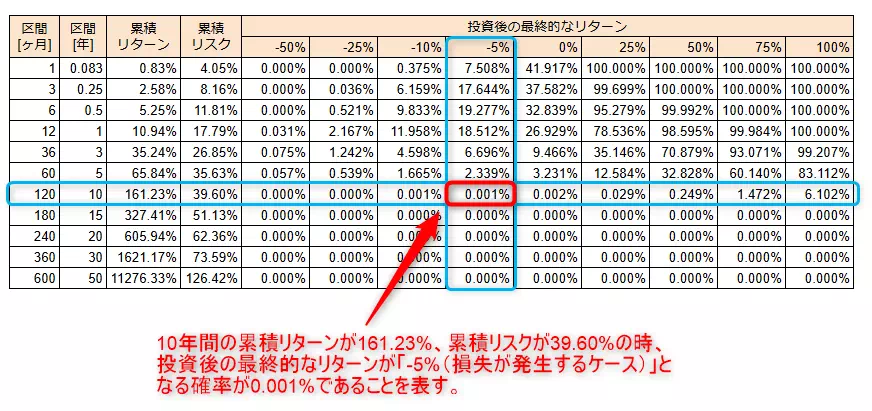
上記の場合、最終的なリターンが $-5$ %になる確率が0.001%となっているため、投資をしても損失が発生する可能性があります。

一方、15年以上投資期間を確保することで、元本割れする確率（最終的なリターンが0%以下になる確率）が0%になっています。

この結果から、15年以上の投資期間を確保することが重要であると予想できますね。

残りの投資期間が短い場合

投資期間が15年確保できない場合は、リスクの低い資産に組み替えることが重要です。

先ほど示したように、投資期間が短い場合、元本割れする確率が高くなるためです。

適切な資産配分（アセットアロケーション）を知りたい方は、当サイトで公開している投資シミュレーターを活用してください。

おすすめ！平均利回りに基づく長期つみたて投資シミュレーターの紹介

新NISAで投資を始める前に、オールカントリー（オルカン）やS&P500などの平均利回りに基 ...

期待リターンと想定リスクを参考に資産形成しよう！

今回は、以下の内容について解説しました。

資産運用により、将来的なリターンが期待できる一方で、それ相応のリスクを取ることになります。

自分のリスク許容度の範囲内で投資を行う為にも、投資対象の期待リターンと想定リスクを知ることは重要です。

こういった経緯もあり、今回は、S&P500を題材に過去データに基づいて、期待リターンと想定リスクを推定しました。

上記の結果から分かるように、S&P500の場合は、15年以上投資を続ければ元本割れする確率がほとんどない、と考えられます。

このような客観的なデータを用いて、投資対象の善し悪しを判断するようにしてみてください。

≫松井証券で証券口座を開設する！