今回は、過去50年間以上のデータを用いて年平均利回りの平均値や投資シミュレーション結果について解説します。
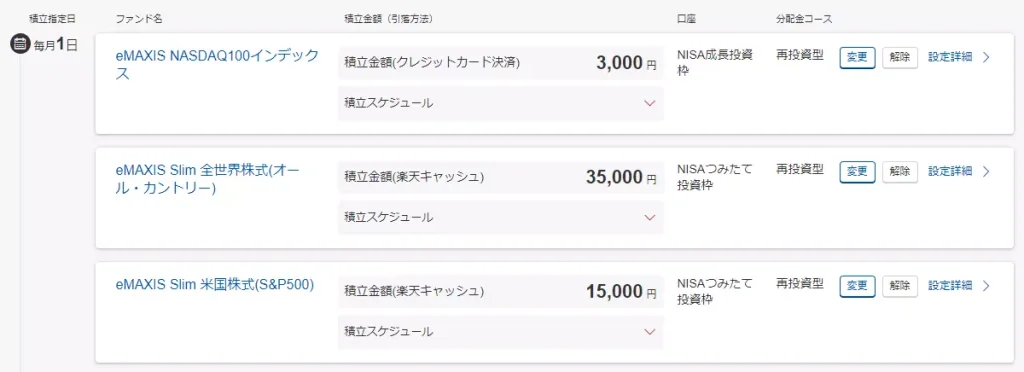
私は、今回の過去実績も参考にして、新NISAにおける投資先を決めています。
記事前半ではS&P500の概要と年平均利回りの計算方法を、後半では投資シミュレーション結果を解説します。
この記事を書いた人
- 『NISAの達人』の管理人
- 会社員＆ブロガー
- 新NISA（選び方、買い方、運用方法）について発信
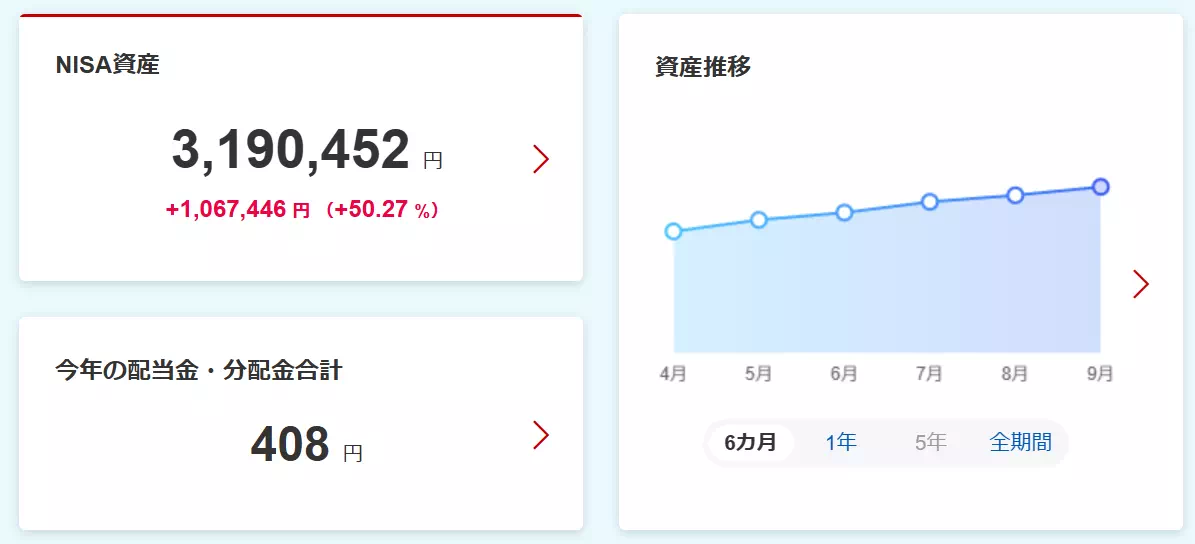
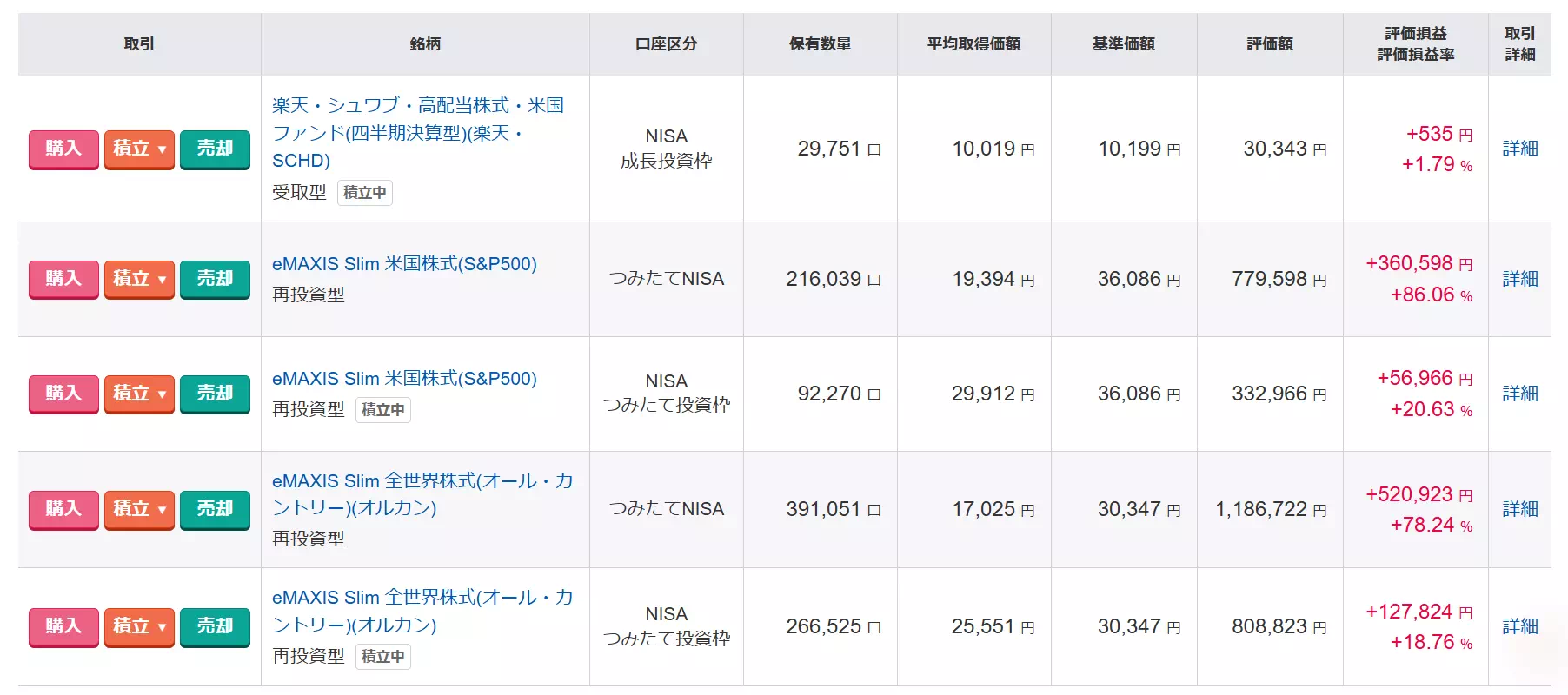
この記事を読み終えることで、実際のデータに基づく年平均利回りを知ることができるだけではなく、具体的な投資結果を用いることで投資先としての善し悪しを判断できるようになります。
これから資産運用を始める方
NISAなど資産運用を始めるには、証券口座の開設が必要です。
また、証券口座を開設するなら、取引コストを抑えられる松井証券
がおすすめ！
この機会に、証券口座を開設しておくことをおすすめします！
S&P500インデックスの概要
まずは、以下の2点に基づいて、S&P500インデックスの概要を解説します。
S&P500インデックスの概要（観点2つ）
S&P500インデックスって何？
S&P500インデックスとは、米国を代表する株価指数（インデックス）の1つで、米国の主要取引所（NASDAQ、ニューヨーク証券取引所など）に上場している企業約500社が対象となっています。
特に、S&P500インデックスに採用される企業は、一定額以上の時価総額があることや4四半期連続で黒字の利益を維持していることなど、厳格な基準を満たすことが挙げられます。
以降では、具体例を取り上げつつS&P500インデックスの特徴について解説します。
S&P500インデックスの特徴は？
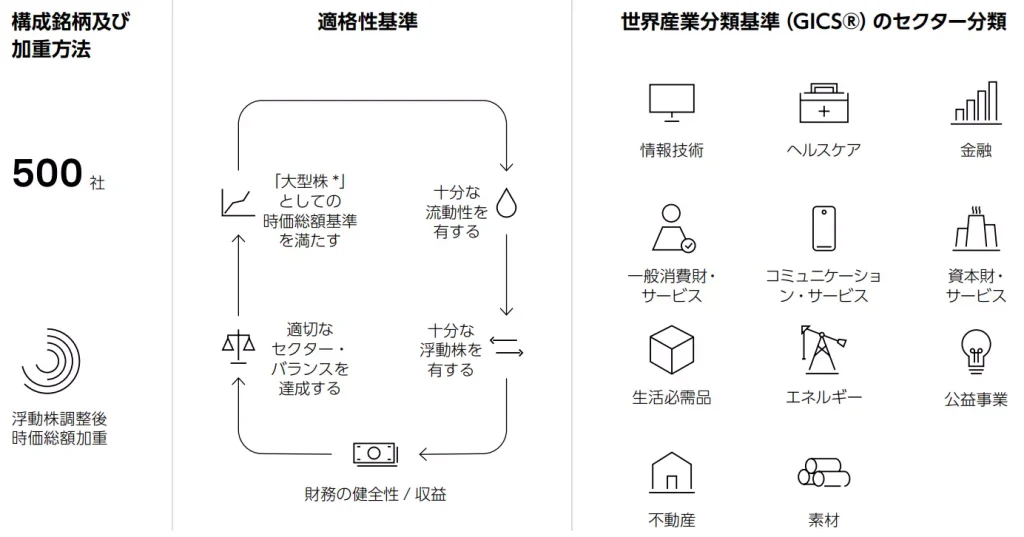
S&P500の特徴として、次の6つが挙げられます。
S&P500の特徴6つ
- 米国企業である
- セクターごとに分散されている
- 大型株に該当する
- 流動性が高い
- 公開株式が十分存在する
- 財務が健全である
また、S&P500のセクター別の内訳は、以下に示す通りです。
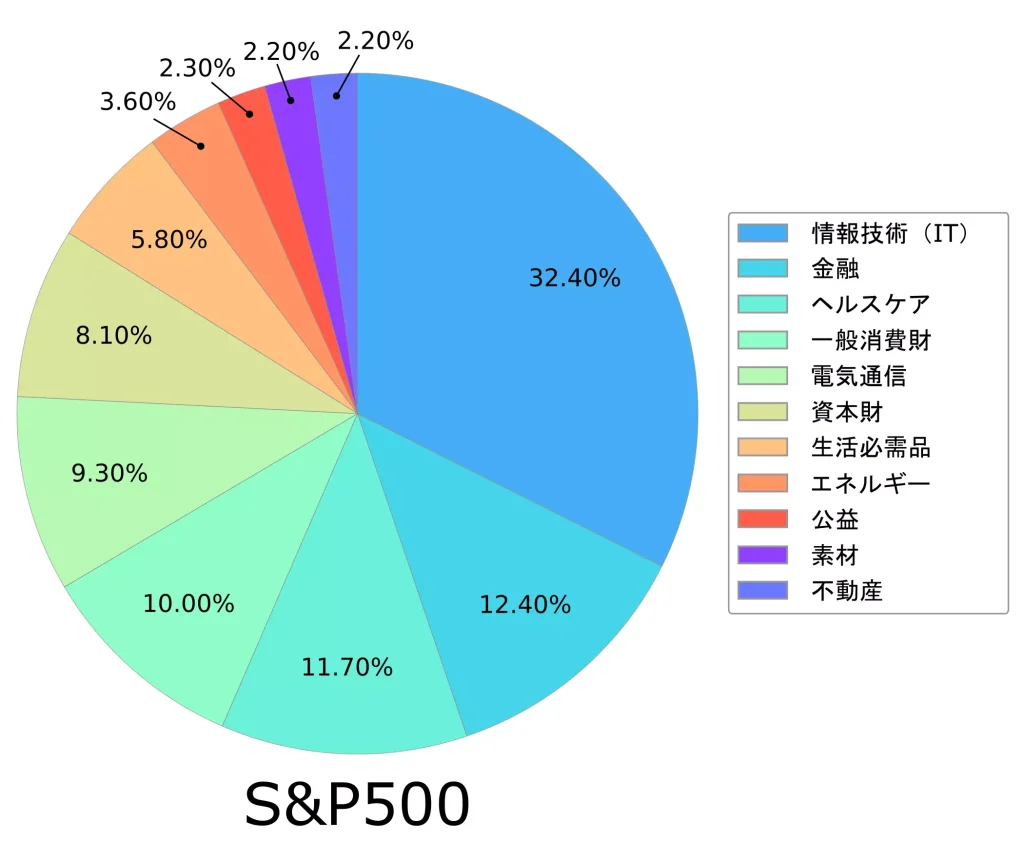
情報技術（IT）が主要なセクターとなりますが、ヘルスケアや生活必需品など、景気の影響を受けづらい銘柄も投資対象に含まれています。
この記事では、このような特徴を持つS&P500の年平均利回りの平均値を過去50年以上のデータを用いて算出した結果や、得られた結果に基づく投資シミュレーションの結果を紹介します。
年平均利回りの平均値の計算方法
過去の年平均利回りの平均値を考える上で、まずは計算方法を理解する必要があります。
今回は、下記の2ステップで年平均利回りの平均値の計算方法を解説します。
【2ステップ】年平均利回りの平均値の計算
具体的な計算式
この記事では、過去の株価データを用いて、次の5ステップで年平均利回りの平均値を算出します。
年平均利回りの平均値の求め方5ステップ
- 投資開始時期 $y$ と投資期間 $n$ を決める。
- 過去の株価データを用いて、以下の式で投資期間における利回り $R_{n}(y)$ を計算する。
ここで、$v(t)$ は評価時期 $t$ における株価を表す。$$
R_{n}(y) = \frac{v(y + n)}{v(y)} \tag{1}
$$ - 算出した利回り $R_{n}(y)$ を用いて、以下の式で年平均利回り $r_{n}(y)$ を計算する。
$$
r_{n}(y) = \left\{ R_{n}(y) \right\}^{\frac{1}{n}} - 1 \tag{2}
$$ - 株価データが存在する範囲内で投資開始時期を1つずつズラしながら、式 $(1), (2)$ の計算を行い、年平均利回りの数列 $\{ r_{n}(k) \}, (k = y_{\textrm{min}}, y_{\textrm{min}} + 1, \cdots, y_{\textrm{max}} - n)$ を得る。
ここで、$y_{\textrm{min}}, y_{\textrm{max}}$ はそれぞれ、過去の株価データの最初の年と最後の年を表す。 - 下記の式から、投資期間 $n$ における年平均利回りの平均値 $ \widehat{r_{n}} $ とする。
$$
\widehat{r_{n}} = \frac{1}{y_{\textrm{max}} - y_{\textrm{min}} - n + 1} \sum_{k = y_{\textrm{min}}}^{y_{\textrm{max}} - n} r_{n}(k) \tag{3}
$$
数式ばかりでイメージが付きづらいと思うので、具体的な数値を用いて年平均利回りの平均値を計算したいと思います。
年平均利回りの平均値の計算例
今回は、以下の架空のデータを用いて、年平均利回りの平均値の計算例を示します。
また、投資開始時期は1950年（$ y = 1950 $）、投資時期は3年（$ n = 3 $）とします。
| 評価時期 $t$ | 株価 $ v(t) $ |
|---|---|
| 1950 | 80 |
| 1951 | 88 |
| 1952 | 104 |
| 1953 | 100 |
| 1954 | 99 |
| 1955 | 91 |
| 1956 | 90 |
先ほど説明した手順において、式 $ (1), (2) $ から、年平均利回りの数列 $ \{ r_{3}(k) \}, (k = 1950, \cdots, 1953) $ は以下のように計算できます。
| 投資開始時期 $y$ | 利回り $ R_{3}(y) $ | 年平均利回り $ r_{3}(y) $ |
|---|---|---|
| 1950 | $ R_{3}(1950) = \frac{100}{80} = 1.25 $ | $ r_{3}(1950) = (1.25)^{1 / 3} - 1 \approx 0.0772 $ |
| 1951 | $ R_{3}(1951) = \frac{99}{88} = 1.125 $ | $ r_{3}(1951) = (1.125)^{1 / 3} - 1 \approx 0.0400 $ |
| 1952 | $ R_{3}(1952) = \frac{91}{104} = 0.875 $ | $ r_{3}(1952) = (0.875)^{1 / 3} - 1 \approx -0.0435 $ |
| 1953 | $ R_{3}(1953) = \frac{90}{100} = 0.9 $ | $ r_{3}(1953) = (0.9)^{1 / 3} - 1 \approx -0.0345 $ |
スペースの都合上、$ \frac{1}{3} $ を $ 1/ 3 $ として表記しました。
式 $ (3) $ から、年平均利回りの平均値 $ \widehat{r_{3}} $ は、
$$
\begin{align}
\widehat{r_{3}} & = \frac{1}{4} \left( 0.0772 + 0.04 - 0.0435 - 0.0345 \right) \\
& = 0.0098 \, (= 0.98\%)
\end{align}
$$
となるため、約1%の利回りが期待できることが分かりますね。
過去50年間以上のデータに基づく利回り実績
今回は、1927年～2023年までの97年間の過去データ（S&P500の過去の株価データ）を用いて、年平均利回りとその平均値を算出します。
また、株価データはコチラのサイトで公開されているものを用いました。
1926年12月の株価を100としています。
以降では、以下の3つの視点で算出した年平均利回りについて深堀します。
算出した年平均利回りについて深堀する際の視点3つ
投資期間ごとの年平均利回りの変動幅
投資期間 $n$ を1年、3年、5年、10年、15年、20年、30年、50年と変化させた場合における年平均利回りの変動幅を算出しました。
変動幅の最大値と最小値をグラフ化した結果は、以下に示す通りです。
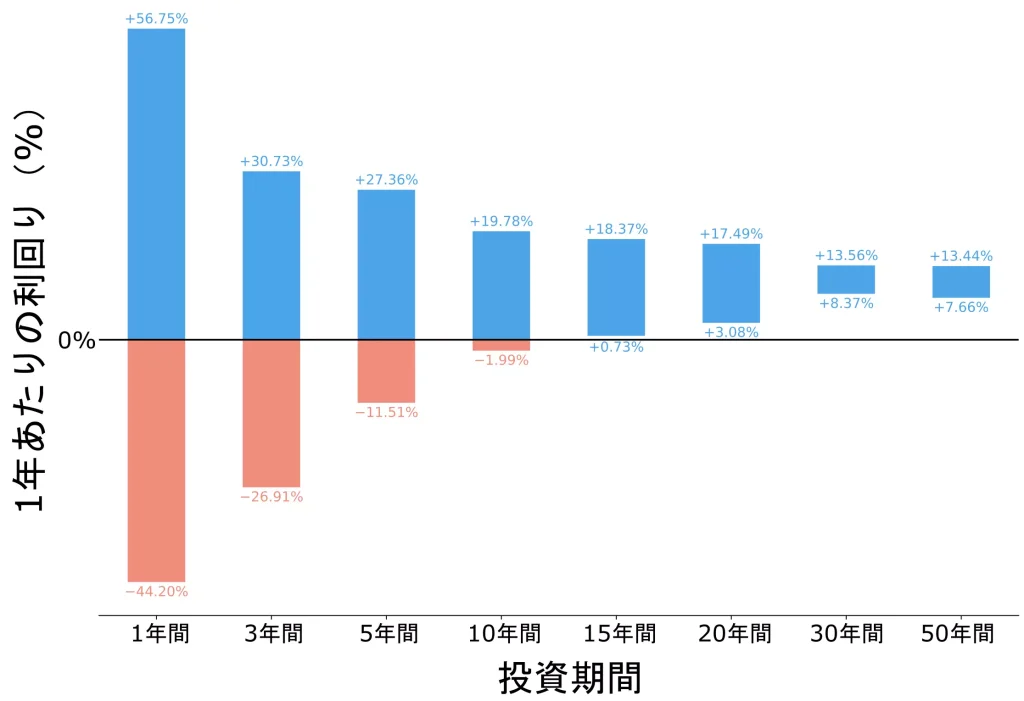
算出結果から、15年以上投資期間を確保すれば、いつ投資を初めても利益が出ることが分かりますね。
投資開始時期ごとの年平均利回りの分布
先程のグラフからも分かるように、投資期間を50年間確保したとしても、年平均利回りは7.66%～13.44%と幅があります。
これは、投資開始時期の違いにより最終的な利回りが異なるためです。
以降では、投資開始時期の違いによる年平均利回りの分布をグラフ化したいと思います。
投資開始時期ごとの年平均利回りの分布
1927年～1976年の50年間における年平均利回りの分布
1927年～1976年の50年間で投資をした場合における、年平均利回りの分布は以下のようになりました。
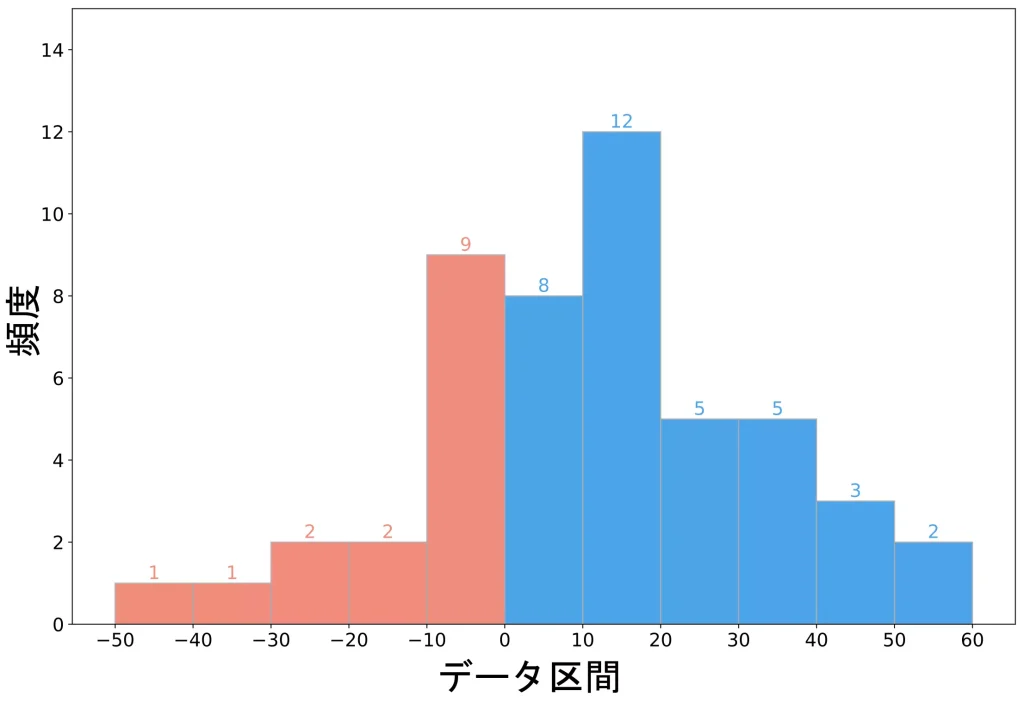
年平均利回りが $+60\%$ となる年もあれば、$-50\%$ となる年もあることが分かりますね。
また、過去実績としては、$+10\%$ ～ $+20\%$ の範囲内にあるデータが最も多く、全体的にプラスリターンに寄っていることが読み取れます。
1951年～2000年の50年間における年平均利回りの分布
同様の方法により、1951年～2000年の50年間で投資をした場合における、年平均利回りの分布は以下のようになりました。
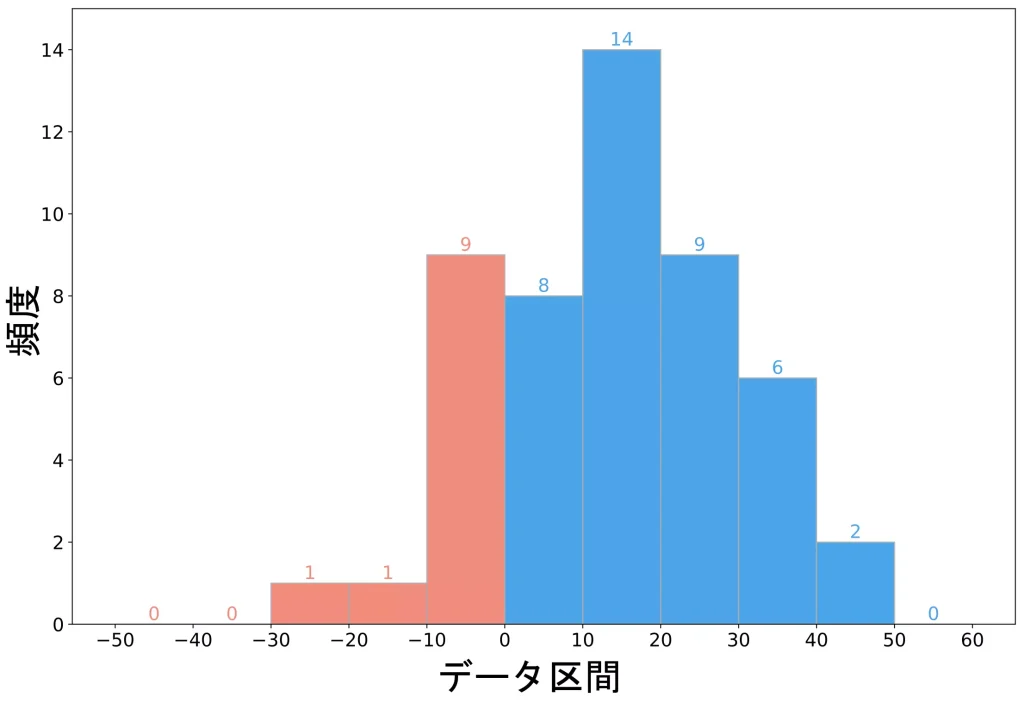
$-30\%$ 以上の利回りとなった年が存在しないことが分かりますね。
今回も $+10\%$ ～ $+20\%$ の範囲内にあるデータが最も多く、全体的にプラスリターンに寄っていることが読み取れます。
1974年～2023年の50年間における年平均利回りの分布
最後に、1974年～2023年の50年間で投資をした場合における、年平均利回りの分布は以下のようになりました。
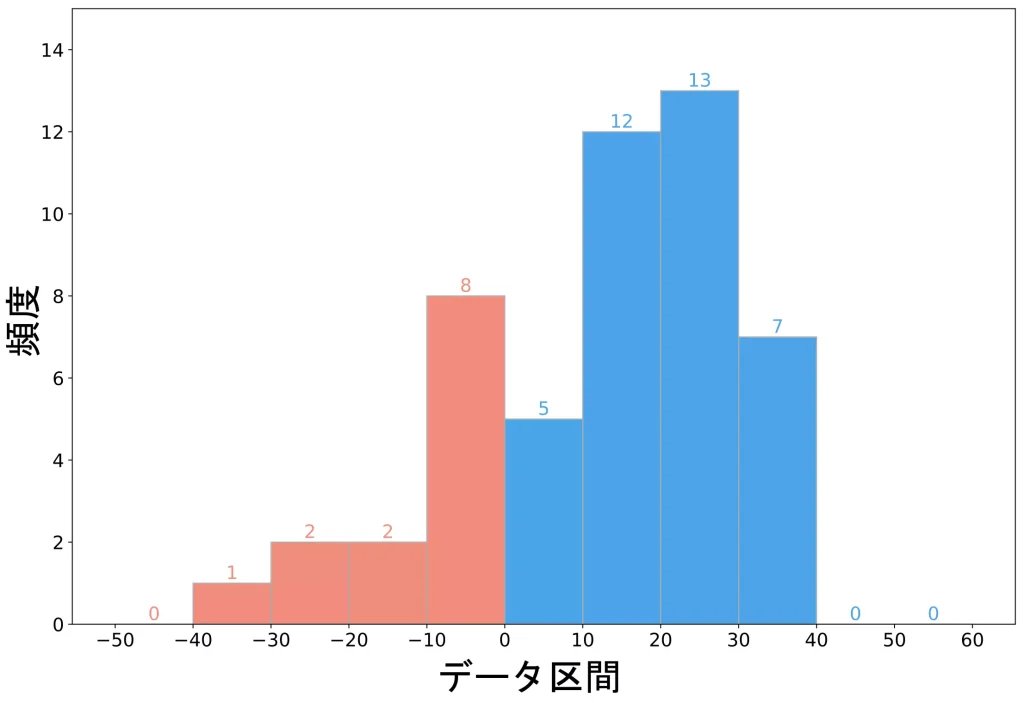
$-10\%$ 以上の利回りとなった時が5年間のみであることが分かりますね。
この期間では、$+20\%$ ～ $+30\%$ の範囲内にあるデータが最も多く、分布もプラスリターンに寄っていることが読み取れます。
以上から、投資開始時期の違いにより、年平均利回りの分布や最終的な利回りが異なることが分かったと思います。
投資期間ごとの年平均利回り推移と平均値
平均利回りの分布に違いがあることを考えると、年平均利回りの推移やその平均値が気になります。
そこで、投資開始時期ごと50年間投資した際の年平均利回りの推移をグラフ化しました。
得られたグラフは以下に示す通りです。
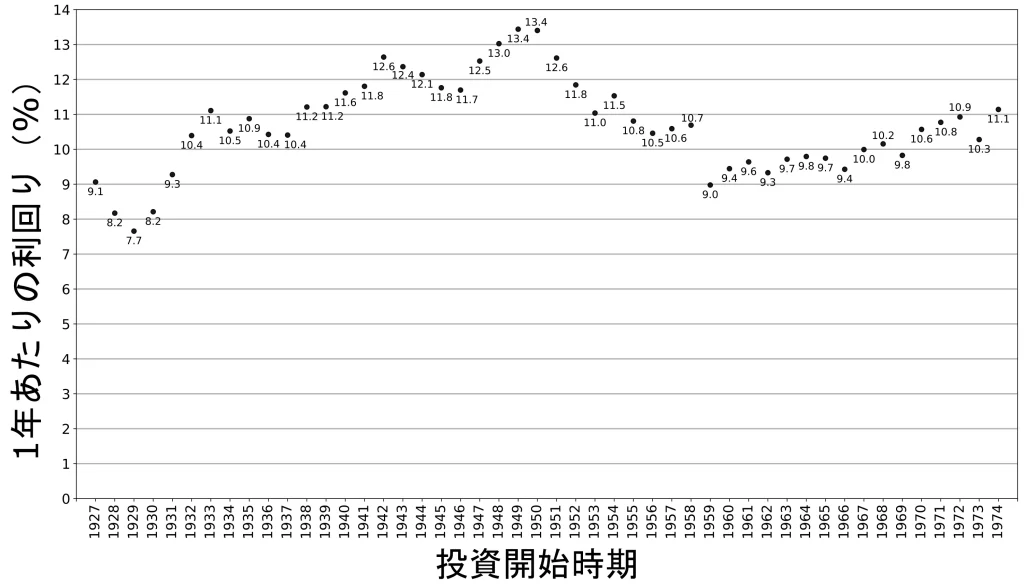
また、投資期間ごとの年平均利回りの平均値と標準偏差（リスク）の平均値は、以下のようになりました。
| 投資期間 | 年平均利回りの平均値 | 標準偏差の平均値 |
|---|---|---|
| 3年間 | 10.468663% | 14.900569 |
| 5年間 | 10.254467% | 12.096647 |
| 10年間 | 10.483210% | 10.523620 |
| 15年間 | 10.520297% | 10.200878 |
| 20年間 | 10.707073% | 10.231159 |
| 30年間 | 11.010443% | 10.393472 |
| 50年間 | 10.714010% | 10.051249 |
投資期間が1年の場合は変動幅が大きすぎたため、除外しております。
上記の結果から、平均して10%程度の利回りが期待できることが分かりますね。
過去50年間以上のデータを用いた投資シミュレーション
ここまでで、過去50年間以上のデータを用いて、年平均利回りの平均値を算出しました。
得られた結果を踏まえて、読者の皆さんは「じゃあ、実際に投資していた場合、どんな結果になったの？」と思うでしょう。
私も同様の疑問を持ったので、過去データを用いた投資シミュレーション結果を紹介します。
今回は、実際に動かして確認できる投資シミュレーターも用意しました。
また、今回用いた分析ツールの詳細は、以下の記事で詳しく解説しています。
シミュレーション条件
まず、今回の投資シミュレーションの条件を定義します。
具体的な条件は以下に示す通りです。
| 項目 | 値 |
|---|---|
| 元金 | 1万円 |
| 毎月の積立額 | 3万円 |
| 投資期間 $n$ | 20年間 |
| 手数料（信託報酬） | 年率0.09372% |
| 投資開始時期の候補 | $1927,1928, \cdots, 2003$ |
| 年平均利回りの平均値 | 10.707073% |
| 標準偏差 | 10.231159 |
年平均利回りの平均値は、月換算すると約0.00851249%になります。
また、$m$ ヶ月目における資産評価額を $p_{m}$、株価を $v(m)$、毎月の積立額を $a$、毎月の手数料を $c$ とおくと、$m + 1$ ヶ月目における資産評価額を $p_{m + 1}$ は、以下のように計算できます。
$$
p_{m + 1} = \left\{ \frac{v(m + 1)}{v(m)} - c \right\} p_{m} + a
$$
過去実績に基づくシミュレーション結果
今回のシミュレーションでは、年平均利回りでの運用実績に加え、投資期間中の最大利回りと最小利回りにおける運用実績もグラフ化しました。
上記の条件でシミュレーションした結果は、以下に示す通りです。
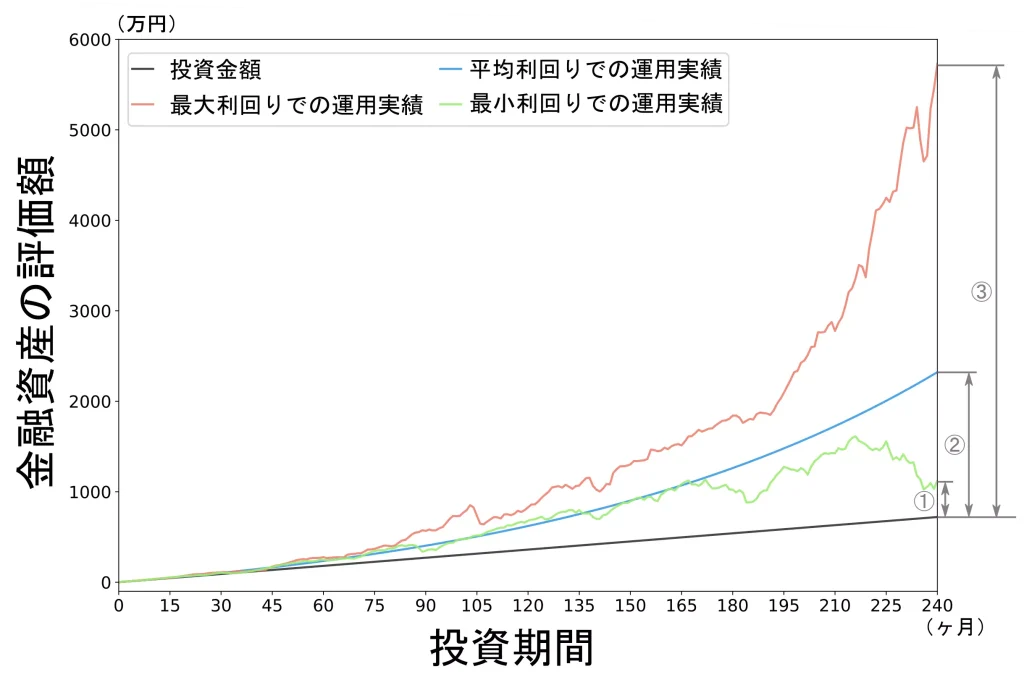
また、最終的な投資結果は以下のようになりました。
| グラフ化対象 | 投資結果 | リターン（概算） |
|---|---|---|
| 積立総額 | 721万円 | - |
| 最小利回りでの運用実績 | 1123万6144円 | 約400万円（図中①部分） |
| 平均利回りでの運用実績 | 2321万7679円 | 約1600万円（図中②部分） |
| 最大利回りでの運用実績 | 5929万1223円 | 約5000万円（図中③部分） |
この結果から、20年間投資期間を確保できれば、最低でも約400万円ほどのリターンが期待できることが分かりますね。
分析ツールによるシミュレーション結果
過去実績と同程度の成績が期待できると仮定した場合、将来的なリターンも気になります。
今回は、当サイトで公開しているツールを用いてシミュレーションした結果も紹介します。
ツールによるシミュレーション結果は、以下に示す通りです。
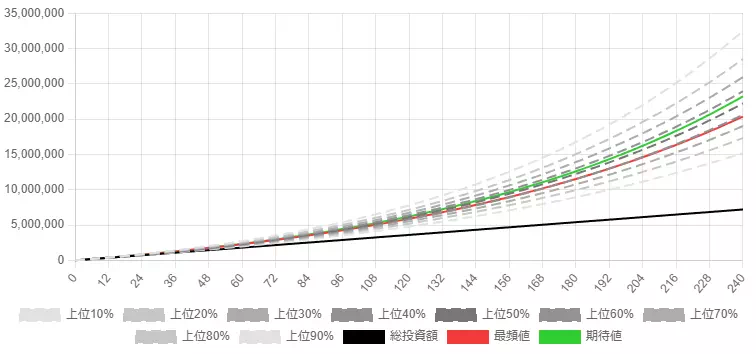
ここで、各項目の具体的な設定値は以下のように設定しています。
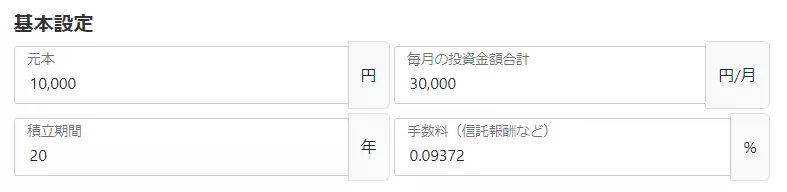
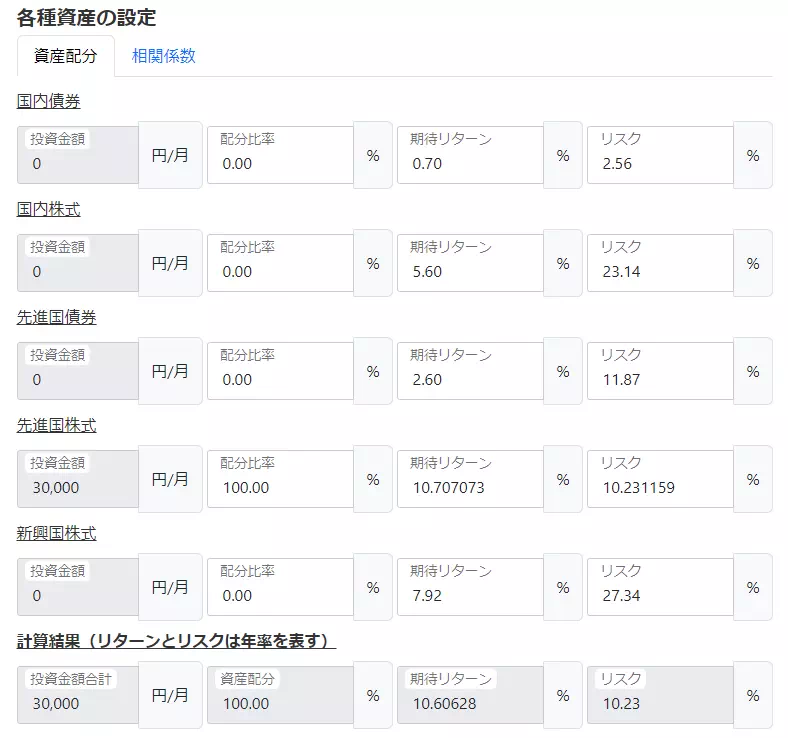
また、シミュレーション結果のサマリーとして以下の結果が得られました。
| 項目 | 値 |
|---|---|
| 総投資額 | 7,210,000円 |
| 運用結果の最頻値 | 20,359,614円 |
| 運用結果の中央値 | 22,226,583円 |
| 運用結果の期待値 | 23,223,319円 |
| 期待値が出る確率 | 44.1% |
| 元本割れする確率 | 0.0% |
今回の条件における試算結果では、元本割れすることがないことが分かりますね。
【体験版】過去実績に基づく投資シミュレーター
最後に、今回の過去データに基づいて実際に投資した際の結果をシミュレーションするツールを作りました。
毎月の投資額や投資期間などを変更してみて、結果がどの様に変わるか試してみてください。
| 具体的な操作方法 | 見た目の変化 |
|---|---|
| Ctrlキーを押しながらマウススクロール | 拡大・縮小 |
| Ctrlキーを押しながらドラッグ＆ドロップ | グラフの移動 |
| ドラッグ＆ドロップ | 選択範囲の拡大・縮小 |
| ピッチ操作（スマホ・タブレット） | 拡大・縮小 |
自分のペースでコツコツ投資しよう！
今回は、以下について解説しました。
過去のデータを用いて、具体的な年平均利回りを算出した結果、平均的な利回りは10%ほどであることが分かりました。
15年以上投資期間を確保できれば、プラスリターンになることも分かりましたね。
今回の結果は今後の投資成績を保証するものではありませんが、これから投資する場合や投資先を決める際の参考になったと思います。
ご自身のリスク許容度も考慮しつつ、新NISAを活用してコツコツと投資をしていってみてください。
これから資産運用を始める方
NISAなど資産運用を始めるには、証券口座の開設が必要です。
また、証券口座を開設するなら、取引コストを抑えられる松井証券がおすすめ！
この機会に、証券口座を開設しておくことをおすすめします！